【题目】若直角三角形
的两条直角边
、
的长分别是
和
，则此直角三角形外接圆半径为________
，内切圆半径为________．
【答案】6.52
【解析】
（1）首先根据90°所对的弦是直径，因而利用勾股定理求出Rt△ABC斜边AB的长，即为直径，那么半径也即可得知．
（2）假设Rt△ABC内切圆P的半径为r，通过图可观察得到内切圆半径与Rt△ABC各边间的关系，列出关系式13=17-2r．从而解得r即为所求．
（1）在Rt△ABC内，AB=
（cm）,
∵AB是Rt△ABC外接圆的直径,
∴Rt△ABC外接圆的半径为6.5（cm）,
（2）设Rt△ABC内切圆P的半径为r．
AE=AM=AC-r=5-r，BE=BN=BC-r=12-r,
AB=AE+BE=（5-r）+（12-r）=17-2r,
∴13=17-2r，
即r=2,
故答案为6.5，2．
科目：初中数学 来源： 题型：
【题目】△ABC是等边三角形，点E、F分别为射线AC、射线CB上两点，CE=BF，直线EB、AF交于点D.
（1）当E、F在边AC、BC上时如图，求证：△ABF≌△BCE.
（2）当E在AC延长线上时，如图，AC=10,S△ABC=25
，EG⊥BC于G，EH⊥AB于H，HE=8，EG= .
（3）E、F分别在AC、CB延长线上时，如图，BE上有一点P，CP=BD,∠CPB是锐角，求证：BP=AD.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，点
是线段
上的动点（点与
不重合），分别以
为边向线段的同一侧作正
和正
.
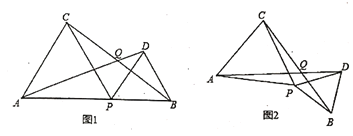
（1）请你判断
与
有怎样的数量关系？请说明理由；
（2）连接
，相交于点
，设
，那么
的大小是否会随点的移动而变化？请说明理由；
（3）如图2，若点固定，将绕点按顺时针方向旋转（旋转角小于
），此时的大小是否发生变化？（只需直接写出你的猜想，不必证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是边长为5cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的速度都为1cm/s．当点P到达点B时，P，Q两点停止运动，设点P的运动时间为t（s）．
（1）当t为何值时，△PBQ是直角三角形？
（2）连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，长方形纸片
中，
，将纸片折叠，使顶点
落在边
上的
点处，折痕的一端
点在边
上.
（1）如图1，当折痕的另一端
在
边上且
时，求
的长
（2）如图2，当折痕的另一端在边上且
时，
①求证：
.②求的长.
（3）如图3，当折痕的另一端在边上，点的对应点在长方形内部，到的距离为2
，且时，求的长.
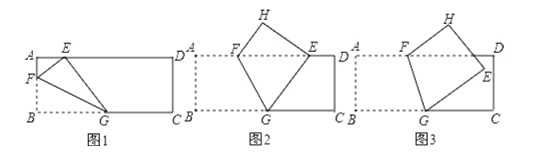
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
的对称轴为
，与
轴的一个交点在
和
之间，其部分图象如图所示，则下列结论：
；
；
点
、
、
是该抛物线上的点，则
；
；
（
为任意实数）．
其中正确结论的个数是（ ）
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点A、B以及直线l，AE⊥l，垂足为点E．
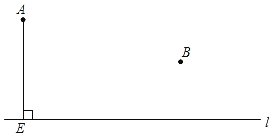
（1）过点B作BF⊥l，垂足为点F；
（2）在直线l上求作一点C，使CA＝CB；
（要求：第（1）、（2）小题用尺规作图，并在图中标明相应字母，保留作图痕迹，不写作法．）
（3）在所作的图中，连接CA、CB，若∠ACB＝90°，求证：△AEC≌△CFB．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）下列四个图都是由16个相同的小正方形拼成的正方形网格，其中的两个小正方形被涂黑.请你在各图中再将两个空白的小正方形涂黑使各图中涂黑部分组成的图形成为轴对称图形(另两个被涂黑的小正方形的位置必须全不相同)，并画出其对称轴。
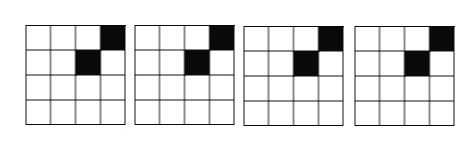
其对称轴分别是： ， ， ， 。
（2）请你发现如图的规律，在空格上画出第4个图案。
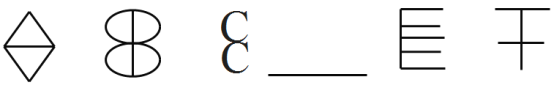
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
