
【题目】已知抛物线过点A(2,0),B(-1,0),与y轴交于点C,且OC=2.则这条抛物线的表达式为( )
A. y=x2-x-2
B. y=-x2+x+2
C. y=x2-x-2或y=-x2+x+2
D. y=-x2-x-2或y=x2+x+2
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB的中点,延长线段AB至点D,使BD=AB,延长AD至点E,使DE=AC.
![]()
(1)依题意画出图形(尺规作图),则![]() =_________(直接写出结果);
=_________(直接写出结果);
(2)若DE=3,求AB的长;
(3)请写出与BE长度相同的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
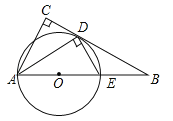
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径.
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=![]() ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)OA= cm,OB= cm.
(2)若点C是线段AO上一点,且满足AC=CO+CB,求CO的长.
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为t(s),当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP﹣OQ=8.
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后立即返回,又以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
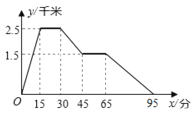
【题目】如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有________.
①.体育场离小冬家2.5千米 ②.小冬在体育场锻炼了15分钟
③.体育场离早餐店4千米 ④.小冬从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
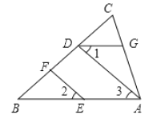
解:因为EF∥AD
所以∠2= ( )
又因为∠1=∠2
所以∠1=∠3( )
所以AB∥ ( )
所以∠BAC+ =180°( )
因为∠BAC=70°
所以∠AGD= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com