
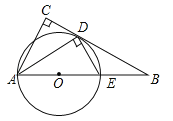
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径.
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=![]() ,AE=4,求CD.
,AE=4,求CD.
【答案】(1)BC与⊙O相切;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)结论:BC与⊙O相切,连接OD只要证明OD∥AC即可.
(2)欲证明△ABD∽△DBE,只要证明∠BDE=∠DAB即可.
(3)在Rt△ODB中,由cosB=![]() =
=![]() ,设BD=
,设BD=![]() k,OB=3k,利用勾股定理列出方程求出k,再利用DO∥AC,得
k,OB=3k,利用勾股定理列出方程求出k,再利用DO∥AC,得![]() 列出方程即可解决问题.
列出方程即可解决问题.
试题解析:(1)结论:BC与⊙O相切.
证明:如图连接OD.
∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠CAB,∴∠CAD=∠DAB,∴∠CAD=∠ADO,∴AC∥OD,∵AC⊥BC,∴OD⊥BC,∴BC是⊙O的切线.
(2)∵BC是⊙O切线,∴∠ODB=90°,∴∠BDE+∠ODE=90°,∵AE是直径,∴∠ADE=90°,∴∠DAE+∠AED=90°,∵OD=OE,∴∠ODE=∠OED,∴∠BDE=∠DAB,∵∠B=∠B,∴△ABD∽△DBE.
(3)在Rt△ODB中,∵cosB=![]() =
=![]() ,设BD=
,设BD=![]() k,OB=3k,∵OD2+BD2=OB2,∴4+8k2=9k2,∴k=2,∴BO=6,BD=
k,OB=3k,∵OD2+BD2=OB2,∴4+8k2=9k2,∴k=2,∴BO=6,BD=![]() ,∵DO∥AC,∴
,∵DO∥AC,∴![]() ,∴
,∴![]() ,∴CD=
,∴CD=![]() .
.


科目:初中数学 来源: 题型:
【题目】某农机租赁公司共有50台收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往A,B两地区收割水稻,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800元 | 1600元 |
B地区 | 1600元 | 1200元 |
![]() 设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
![]() 若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
![]() 农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号max﹛a , b﹜的含义为:当a≥b时, max﹛a , b﹜=a;当a<b时,max﹛a , b﹜=b.如 max﹛2 , -3﹜=2 , max﹛-4 , -2﹜=-2,则max﹛-x2+2x+3 , |x|﹜的最小值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】营市公交公司将淘汰所有线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.(1)求证: AE=AF; (2)若AG=4,AC=7,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一列有理数-1,2,-3,4,-5,6,……,如图所示有序排列.根据图中的排列规律可知,“峰1” 中峰顶的位置(C的位置)是有理数4,那么,“峰5”中C 的位置是有理数 ,2017应排在A、E中 的位置.其中两个填空依次为
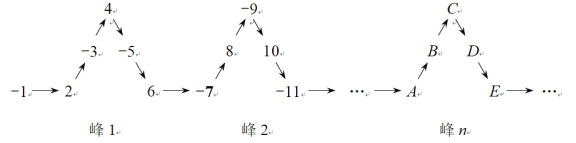
A.24 , AB.﹣24, AC.25, ED.﹣25, E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
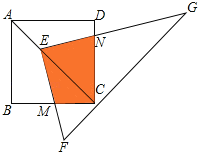
A.![]() a2 B.
a2 B.![]() a2 C.
a2 C.![]() a2 D.
a2 D.![]() a2
a2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三学生组织甲、乙两个旅行团去某景点旅游,已知甲团人数少于50人,乙团人数不超过100人.下面是小明与其他两位同学交流的情况.根据他们的对话,组织者算了一下,若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计应付门票费1080元.



(1)请你判断乙团的人数是否也少于50人.
(2)求甲、乙两旅行团各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com