
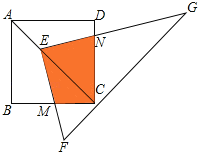
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A.![]() a2 B.
a2 B.![]() a2 C.
a2 C.![]() a2 D.
a2 D.![]() a2
a2
【答案】D.
【解析】
试题分析:过E作EP⊥BC于点P,EQ⊥CD于点Q,△EPM≌△EQN,利用四边形EMCN的面积等于正方形PCQE的面积求解.
解:过E作EP⊥BC于点P,EQ⊥CD于点Q,
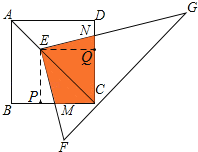
∵四边形ABCD是正方形,
∴∠BCD=90°,
又∵∠EPM=∠EQN=90°,
∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG是直角三角形,
∴∠NEF=∠NEQ+∠MEQ=90°,
∴∠PEM=∠NEQ,
∵AC是∠BCD的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形,
在△EPM和△EQN中,
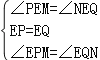 ,
,
∴△EPM≌△EQN(ASA)
∴S△EQN=S△EPM,
∴四边形EMCN的面积等于正方形PCQE的面积,
∵正方形ABCD的边长为a,
∴AC=![]() a,
a,
∵EC=2AE,
∴EC=![]() a,
a,
∴EP=PC=![]() a,
a,
∴正方形PCQE的面积=![]() a×
a×![]() a=
a=![]() a2,
a2,
∴四边形EMCN的面积=![]() a2,
a2,
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(探索新知)如图1,点![]() 在线段
在线段![]() 上,图中共有3条线段:
上,图中共有3条线段:![]() 、
、![]() 、和
、和![]() ,若其中有一条线段的长度是另一条线段长度的两倍,则称点
,若其中有一条线段的长度是另一条线段长度的两倍,则称点![]() 是线段
是线段![]() 的“二倍点”.
的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)如图2,点![]() 表示数-10,点
表示数-10,点![]() 表示数20,若点
表示数20,若点![]() 从点
从点![]() ,以每秒3
,以每秒3![]() 的速度向点
的速度向点![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 时停止运动,设运动的时间为
时停止运动,设运动的时间为![]() 秒.
秒.
(2)点![]() 在运动过程中表示的数为 (用含
在运动过程中表示的数为 (用含![]() 的代数式表示);
的代数式表示);
(3)求![]() 为何值时,点
为何值时,点![]() 是线段
是线段![]() 的“二倍点”;
的“二倍点”;
(4)同时点![]() 从点
从点![]() 的位置开始,以每秒2
的位置开始,以每秒2![]() 的速度向点
的速度向点![]() 运动,并与点
运动,并与点![]() 同时停止.请直接写出点
同时停止.请直接写出点![]() 是线段
是线段![]() 的“二倍点”时
的“二倍点”时![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
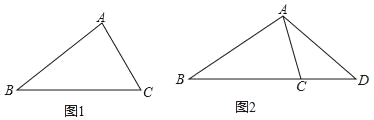
【题目】问题背景 如图1,在△ABC中,BC=4,AB=2AC.
问题初探 请写出任意一对满足条件的AB与AC的值:AB= ,AC= .
问题再探 如图2,在AC右侧作∠CAD=∠B,交BC的延长线于点D,求CD的长.
问题解决 求△ABC的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
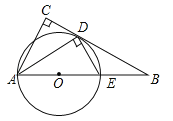
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径.
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=![]() ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上原点为O,点P表示的数为30,点Q表示的数为120,甲、乙两只小虫分别从O,P两点出发,沿直线匀速爬向点Q,最终达到点Q.已知甲每分钟爬行60个单位长度,乙每分钟爬行30个单位长度,则在此过程中,甲、乙两只小虫相距10个单位长度时的爬行时间为_________分钟.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里:
1,﹣![]() ,8.9,﹣7,
,8.9,﹣7, ![]() ,﹣3.2,+1 008,﹣0.06,28,﹣9.
,﹣3.2,+1 008,﹣0.06,28,﹣9.
正整数集合:{______…};
负整数集合:{______…};
正分数集合:{______…};
负分数集合:{______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是![]() ,连接
,连接![]() 交于点O,并分别与边
交于点O,并分别与边![]() 交于点
交于点![]() ,连接AE,下列结论:
,连接AE,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 当
当![]() 时,
时, ![]() ,其中正确结论的个数是
,其中正确结论的个数是![]()

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程.
已知:如图,在RtΔABC中,∠ABC=90°,0为AC的中点.
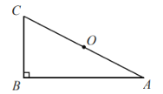
求作:四边形ABCD,使得四边形ABCD为矩形.
作法:①作射线BO,在线段BO的延长线上取点D,使得DO=BO;
②连接AD,CD,则四边形ABCD为矩形.
根据小丁设计的尺规作图过程.
(1)使用直尺和圆规,在图中补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∴点O为AC的中点,
∴AO=CO.
又∵DO=BO,
∵四边形ABCD为平行四边形(__________)(填推理的依据).
∵∠ABC=90°,
∴![]() ABCD为矩形(_________)(填推理的依据).
ABCD为矩形(_________)(填推理的依据).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com