
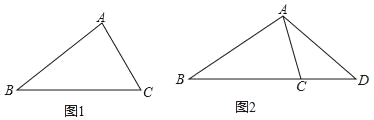
【题目】问题背景 如图1,在△ABC中,BC=4,AB=2AC.
问题初探 请写出任意一对满足条件的AB与AC的值:AB= ,AC= .
问题再探 如图2,在AC右侧作∠CAD=∠B,交BC的延长线于点D,求CD的长.
问题解决 求△ABC的面积的最大值.
【答案】(1)6、3;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)设AC=x,则AB=2x,根据三角形的三边关系,求出x的取值范围,然后取一个符合条件的值即可;
(2)根据两角对应相等的两三角形相似,可证明△DAC∽△DBA,然后根据相似三角形的对应边成比例,代入即可构成方程组求解;
(3)设AC=m、则AB=2m,根据锐角三角函数表示出△ABC的面积,然后由余弦定理,可求得cosC的关系式,再代入面积的关系式,配方后,根据二次函数的最值求解即可.
试题解析:问题初探,设AC=x,则AB=2x,
∵BC=4,
∴2x﹣x<4且2x+x>4,
解得: ![]() <x<4,
<x<4,
取x=3,则AC=3、AB=6,
故答案为:6、3;
问题再探,∵∠CAD=∠B,∠D=∠D,
∴△DAC∽△DBA,
则![]() =
=![]() =
=![]() ,
,
设CD=a、AD=b,
∴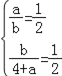 ,
,
解得:![]() ,
,
即CD=![]() ;
;
问题解决,设AC=m、则AB=2m,
根据面积公式可得S△ABC=![]() ACBCsinC=2msinC=2m
ACBCsinC=2msinC=2m![]() ,
,
由余弦定理可得cosC=![]() ,
,
∴S△ABC=2m![]()
=2m![]()
=![]()
=
=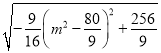
由三角形三边关系知![]() <m<4,
<m<4,
所以当m=![]() 时,S△ABC取得最大值
时,S△ABC取得最大值![]() .
.


科目:初中数学 来源: 题型:
【题目】某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:
(1)洗衣机的进水时间是______分钟,清洗时洗衣机中的水量是_______升.
(2)进水时y与x之间的关系式是____________.
(3)已知洗衣机的排水速度是每分钟18升,如果排水时间为2分钟,排水结束时洗衣机中剩下的水量是____________升.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中
①一个角的两边分别垂直于另一角的两边,则这两个角相等或互补
②若点A在y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一象限
③半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的共有四个
④如果AD是△ABC的高,∠CAD=∠B,那么△ABC是直角三角形
正确命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号max﹛a , b﹜的含义为:当a≥b时, max﹛a , b﹜=a;当a<b时,max﹛a , b﹜=b.如 max﹛2 , -3﹜=2 , max﹛-4 , -2﹜=-2,则max﹛-x2+2x+3 , |x|﹜的最小值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
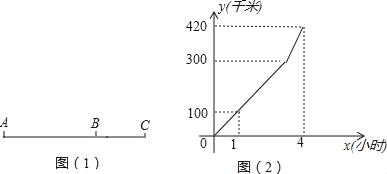
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】营市公交公司将淘汰所有线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.(1)求证: AE=AF; (2)若AG=4,AC=7,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
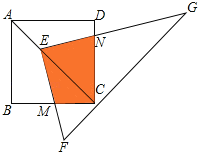
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A.![]() a2 B.
a2 B.![]() a2 C.
a2 C.![]() a2 D.
a2 D.![]() a2
a2
查看答案和解析>>
科目:初中数学 来源: 题型:
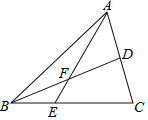
【题目】如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=_____;若S△ABC=12,则S△ADF﹣S△BEF=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com