
【题目】如图,正方形ABCD的边长是![]() ,连接
,连接![]() 交于点O,并分别与边
交于点O,并分别与边![]() 交于点
交于点![]() ,连接AE,下列结论:
,连接AE,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 当
当![]() 时,
时, ![]() ,其中正确结论的个数是
,其中正确结论的个数是![]()

A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】∵四边形ABCD是正方形,AD=BC,∠DAB=∠ABC=90°,∵BP=CQ,∴AP=BQ,在△DAP与△ABQ中,AD=AB,∠DAP=∠ABQ,AP=BQ,∴△DAP≌△ABQ,∴∠P=∠Q,∵∠Q+∠QAB=90°,∴∠P+∠QAB=90°,∴∠AOP=90°,∴AQ⊥DP,则①正确;
∵∠DOA=∠AOP=90,∠ADO+∠P=∠ADO+∠DAO=90°,∴∠DAO=∠P,∴△DAO∽△APO,∴![]() =
=![]() ,所以OA2=OD·OP,∵AE>AB,∴AE>AD,∴OD≠OE,∴OA2≠OEOP;则②错误;
,所以OA2=OD·OP,∵AE>AB,∴AE>AD,∴OD≠OE,∴OA2≠OEOP;则②错误;
在△CQF与△BPE中,∠FCQ=∠EBP,∠Q=∠P,CQ=BP,∴△CQF≌△BPE,∴CF=BE,∴DF=CE,在△ADF与△DCE中,AD=CD,∠ADC=∠DCE,DF=CE,∴△ADF≌△DCE,∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,即S△AOD=S四边形OECF;则③正确;
∵BP=1,AB=3,∴AP=4,∵△AOP∽△DAP,∴![]() =
=![]() =
=![]() ,∴BE=
,∴BE=![]() ,∴QE=
,∴QE=![]() ,∵△QOE∽△PAD,∴
,∵△QOE∽△PAD,∴![]() =
=![]() =
=![]() =
=![]() ,∴QO=
,∴QO=![]() ,OE=
,OE=![]() ,∴AO=5-QO=
,∴AO=5-QO=![]() ,∴tan∠OAE=
,∴tan∠OAE=![]() =
=![]() ,则④错误,故选B.
,则④错误,故选B.


科目:初中数学 来源: 题型:
【题目】下列说法中
①一个角的两边分别垂直于另一角的两边,则这两个角相等或互补
②若点A在y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一象限
③半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的共有四个
④如果AD是△ABC的高,∠CAD=∠B,那么△ABC是直角三角形
正确命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.(1)求证: AE=AF; (2)若AG=4,AC=7,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
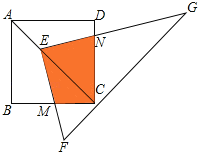
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A.![]() a2 B.
a2 B.![]() a2 C.
a2 C.![]() a2 D.
a2 D.![]() a2
a2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句,画出图形并回答问题.
如图,已知三点A,B,C.

(1)分别作直线AB和射线AC;
(2)作线段BC, 取BC的中点D;
(3)连接AD;
(4)用量角器度量出∠ADB的度数最接近( )
A.80° B. 90° C. 100° D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三学生组织甲、乙两个旅行团去某景点旅游,已知甲团人数少于50人,乙团人数不超过100人.下面是小明与其他两位同学交流的情况.根据他们的对话,组织者算了一下,若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计应付门票费1080元.



(1)请你判断乙团的人数是否也少于50人.
(2)求甲、乙两旅行团各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (
(![]() ,
, ![]() )的图象与直线
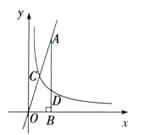
)的图象与直线![]() 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确实一点M,使点M到C、D两点距离之和d=MC+MD,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
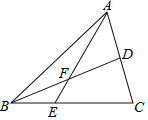
【题目】如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=_____;若S△ABC=12,则S△ADF﹣S△BEF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理
表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理![]() 也可理解为
也可理解为![]() 与3两数在数轴上所对应的两点之间的距离,
与3两数在数轴上所对应的两点之间的距离,![]() 就表示
就表示![]() 在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求![]() .
.
(2)若![]() ,则
,则![]() .
.
(3)请你找出所有符合条件的整数![]() ,使得
,使得![]() .
.
(4)求![]() 的最小值,并写出此时
的最小值,并写出此时![]() 的取值情况.
的取值情况.
(5)已知![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com