练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】根据下列语句，画出图形并回答问题．

    如图，已知三点A，B，C．

    （1）分别作直线AB和射线AC；

    （2）作线段BC, 取BC的中点D；

    （3）连接AD；

    （4）用量角器度量出∠ADB的度数最接近（ ）

    A.80° B. 90° C. 100° D. 110°

    【答案】（1）详见解析；（2）详见解析；（3）详见解析；（4）B.

    【解析】

    （1）根据直线的定义以及射线的定义作图即可；

    （2）根据线段的定义连接BC，然后用刻度尺测量BC的长度，继而得到线段的中点D即可；

    （3）按题意连接AD即可；

    （4）将量角器的中心和角的顶点D对齐，量角器的0刻度线和角的一条边DA对齐，然后看另一条边DB对着的刻度线，准确读数即可得.

    （1）如图所示；

    （2）如图所示；

    （3）如图所示；

    （4）如图，用量角器测量可知∠ADB接近90度，

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    如图，在平面直角坐标系xOy中，点A与点B的坐标分别是，．

    对于坐标平面内的一点P，给出如下定义：如果，则称点P为线段AB的“等角点”显然，线段AB的“等角点”有无数个，且A、B、P三点共圆．

    设A、B、P三点所在圆的圆心为C，直接写出点C的坐标和的半径；

    轴正半轴上是否有线段AB的“等角点”？如果有，求出“等角点”的坐标；如果没有，请说明理由；

    当点P在y轴正半轴上运动时，是否有最大值？如果有，说明此时最大的理由，并求出点P的坐标；如果没有请说明理由．

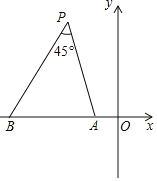
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，OC在∠BOD内．

    （1）如果∠AOC和∠BOD都是直角．

    ①若∠BOC=60°，则∠AOD的度数是　 　；

    ②猜想∠BOC与∠AOD的数量关系，并说明理由；

    （2）如果∠AOC=∠BOD=x°，∠AOD=y°，求∠BOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上原点为O，点P表示的数为30，点Q表示的数为120，甲、乙两只小虫分别从O，P两点出发，沿直线匀速爬向点Q，最终达到点Q.已知甲每分钟爬行60个单位长度，乙每分钟爬行30个单位长度，则在此过程中，甲、乙两只小虫相距10个单位长度时的爬行时间为_________分钟.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

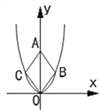
    【题目】二次函数y=的图象如图,点O为坐标原点,点A在y轴的正半轴上，点B、C在二次函数y=的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积为___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长是，连接交于点O，并分别与边交于点，连接AE，下列结论： ； ； ； 当时， ，其中正确结论的个数是

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】老师布置了这样一道作业题：

    在△ABC中，AB＝AC≠BC，点D和点A在直线BC的同侧，BD＝BC，∠BAC＝α，∠DBC＝β，α＋β＝120°，连接AD，求∠ADB的度数．

    小聪提供了研究这个问题的过程和思路：先从特殊问题开始研究，当α＝90°，β＝30°时（如图1），利用轴对称知识，以AB为对称轴构造ΔABD的轴对称图形ΔABD′，连接CD′（如图2），然后利用α＝90°，β＝30°以及等边三角形的相关知识便可解决这个问题．

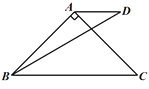
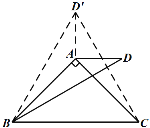
    图1 图2

    （1）请结合小聪研究问题的过程和思路，求出这种特殊情况下∠ADB的度数；

    （2）结合小聪研究特殊问题的启发，请解决老师布置的这道作业题.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

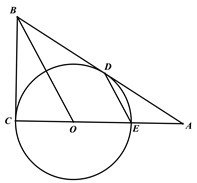
    【题目】如图,在,O是AC上的一点, 与BC,AB分别切于点C,D, 与AC相交于点E,连接BO.

    (1) 求证:CE2=2DEBO;

    (2) 若BC=CE=6,则AE= ,AD= .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为节约用水，某区规定三口之家每月标准用水量为15立方米，不超过标准的水费价格为每立方米1.5元，超过标准的超过部分的价格为每立方米3元，小明家11月份用水x立方米；小红家11月份用水y（y＞15）立方米

    （1）用含y的代数式表示小红家11月份应缴的水费；

    （2）用含有x的代数式表示小明家11月份应缴的水费.

    查看答案和解析>>

    同步练习册答案