
【题目】老师布置了这样一道作业题:
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
小聪提供了研究这个问题的过程和思路:先从特殊问题开始研究,当α=90°,β=30°时(如图1),利用轴对称知识,以AB为对称轴构造ΔABD的轴对称图形ΔABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形的相关知识便可解决这个问题.
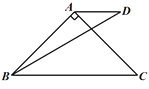
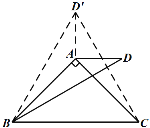
图1 图2
(1)请结合小聪研究问题的过程和思路,求出这种特殊情况下∠ADB的度数;
(2)结合小聪研究特殊问题的启发,请解决老师布置的这道作业题.
【答案】(1)30°(2)30°或150°
【解析】
(1)如图2中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,由△ABD≌△ABD′,推出△D′BC是等边三角形,再证明△AD′B≌△AD′C,得∠AD′B=∠AD′C,由此即可解决问题.
(2)第①种情况:当60°<α≤120°时,如图3中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,证明方法类似(1).第②种情况:当0°<α<60°时,如图4中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′.证明方法类似(1).
(1)如图1作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°
∵∠DBC=30°,

∴∠ABD=∠ABC-∠DBC=15°,
∵AB=AB,∠ABD′=∠ABD,BD′=BD,
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等边三角形,
∴D′B=D′C,∠BD′C=60°,
∵AB=AC,AD'=AD',
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=![]() ∠BD′C=30°,
∠BD′C=30°,
∴∠ADB=30°.
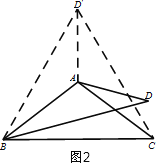
(2)解:第①种情况:当60°<α≤120°时,
如图2,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,
∵AB=AC,∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=![]() ,
,
∴∠ABD=∠ABC-∠DBC=![]() ,
,
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=![]() ,BD=BD′,∠ADB=∠AD′B
,BD=BD′,∠ADB=∠AD′B
∴∠D′BC=∠ABD′+∠ABC=![]() =180°-(α+β),
=180°-(α+β),
∵α+β=120°,
∴∠D′BC=60°,
以下同(1)可求得∠ADB=30°,
第②种情况:当0°<α<60°时,
如图3,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′.

同理可得:∠ABC=![]() ,
,
∴∠ABD=∠DBC-∠ABC=β(90°![]() ),
),
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=β(90°![]() ),BD=BD′,∠ADB=∠AD′B,
),BD=BD′,∠ADB=∠AD′B,
∴∠D′BC=∠ABC-∠ABD′=90°-![]() [β(90°
[β(90°![]() )]=180°(α+β),
)]=180°(α+β),
∴D′B=D′C,∠BD′C=60°.
同(1)可证△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】某校为打造智慧课堂,准备集体购买一批平板电脑,原计划订购60台,每台1000元,商家表示,如果多购,可以优惠,结果校长实际订购了72台,每台减价30元,但商家获得同样多的利润.
(1)求每台平板电脑的成本是多少元?
(2)求商家的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录的是今年长江某一周的水位变化情况,这一周的上周末的水位已达到警戒水位33米(正号表示水位比前一天上升,负号表示水位比前一天下降).
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
水位变化(米) |
|
|
|
|
|
|
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句,画出图形并回答问题.
如图,已知三点A,B,C.

(1)分别作直线AB和射线AC;
(2)作线段BC, 取BC的中点D;
(3)连接AD;
(4)用量角器度量出∠ADB的度数最接近( )
A.80° B. 90° C. 100° D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表三行数的规律,回答下列问题:
第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
(1)第1行的第四个数a是 ;第3行的第六个数b是 ;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为 ;
(3)已知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (
(![]() ,
, ![]() )的图象与直线
)的图象与直线![]() 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
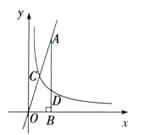
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确实一点M,使点M到C、D两点距离之和d=MC+MD,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办“红歌伴我成长”歌咏比赛活动,参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如图:
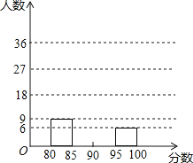
分数段 | 频数 | 频率 |
80≤x<85 | 9 | 0.15 |
85≤x<90 | m | 0.45 |
90≤x<95 | ■ | ■ |
95≤x<100 | 6 | n |
(1)求m,n的值分别是多少;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,连接EF.
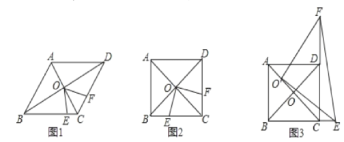
(1)如图2,当∠ABC=60°时,猜想三条线段CE、CF、AB之间的数量关系___;
(2)如图1,当∠ABC=90°时,若AC=4![]() ,BE=
,BE=![]() ,求线段EF的长;
,求线段EF的长;
(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系,请直接写出你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com