
【题目】下表记录的是今年长江某一周的水位变化情况,这一周的上周末的水位已达到警戒水位33米(正号表示水位比前一天上升,负号表示水位比前一天下降).
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
水位变化(米) |
|
|
|
|
|
|
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(﹣6,0),D(﹣7,3),点B、C在第二象限内.
(1)求点B的坐标。
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝网店销售台灯,每个台灯售价为60元,每星期可卖出300个,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30个.已知该款台灯每个成本为40元,
(1)若每个台灯降x元(![]() ),则每星期能卖出 个台灯,每个台灯的利润是 元.
),则每星期能卖出 个台灯,每个台灯的利润是 元.
(2)在顾客得实惠的前提下,该淘宝网店还想获得6480元的利润,应将每件的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=a(cm),其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-CB=b(cm),M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上原点为O,点P表示的数为30,点Q表示的数为120,甲、乙两只小虫分别从O,P两点出发,沿直线匀速爬向点Q,最终达到点Q.已知甲每分钟爬行60个单位长度,乙每分钟爬行30个单位长度,则在此过程中,甲、乙两只小虫相距10个单位长度时的爬行时间为_________分钟.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
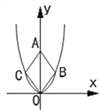
【题目】二次函数y=![]() 的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=![]() 的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为___________.
的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师布置了这样一道作业题:
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
小聪提供了研究这个问题的过程和思路:先从特殊问题开始研究,当α=90°,β=30°时(如图1),利用轴对称知识,以AB为对称轴构造ΔABD的轴对称图形ΔABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形的相关知识便可解决这个问题.
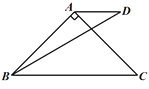
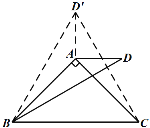
图1 图2
(1)请结合小聪研究问题的过程和思路,求出这种特殊情况下∠ADB的度数;
(2)结合小聪研究特殊问题的启发,请解决老师布置的这道作业题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两校举行初中数学联赛,各校从九年级学生中挑选50人参加,成绩统计如下表:
成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | A | 2 | 5 | 10 | 13 | 14 | 6 |
B | 4 | 4 | 16 | 2 | 12 | 12 | |
请你根据所学知识和表中数据,判断这两校学生在这次联赛中的成绩谁优谁次?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com