
【题目】二次函数y=![]() 的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
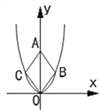
的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=![]() 的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为___________.
的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为___________.
【答案】2![]()
【解析】分析:连结BC交OA于D,如图,根据菱形的性质得BC⊥OA,∠OBD=60°,利用含30度的直角三角形三边的关系得OD=![]() BD,设BD=t,则OD=
BD,设BD=t,则OD=![]() t,B(t,
t,B(t,![]() t),利用二次函数图象上点的坐标特征得
t),利用二次函数图象上点的坐标特征得![]() t2=
t2=![]() t,解得t1=0(舍去),t2=1,则BD=1,OD=
t,解得t1=0(舍去),t2=1,则BD=1,OD=![]() ,然后根据菱形性质得BC=2BD=2,OA=2OD=2
,然后根据菱形性质得BC=2BD=2,OA=2OD=2![]() ,再利用菱形面积公式计算即可.
,再利用菱形面积公式计算即可.
详解:连结BC交OA于D,如图,
∵四边形OBAC为菱形,∴BC⊥OA.
∵∠OBA=120°,∴∠OBD=60°,∴OD=![]() BD,设BD=t,则OD=
BD,设BD=t,则OD=![]() t,∴B(t,
t,∴B(t,![]() t),把B(t,
t),把B(t,![]() t)代入y=
t)代入y=![]() x2得:
x2得:![]() t2=
t2=![]() t,解得:t1=0(舍去),t2=1,∴BD=1,OD=
t,解得:t1=0(舍去),t2=1,∴BD=1,OD=![]() ,∴BC=2BD=2,OA=2OD=2
,∴BC=2BD=2,OA=2OD=2![]() ,∴菱形OBAC的面积=
,∴菱形OBAC的面积=![]() ×2×2
×2×2![]() =2
=2![]() .
.
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
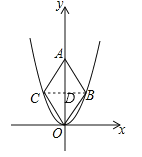
【题目】如图,平面直角坐标系中,点O为坐标原点,矩形OABC的边OA,OC在坐标轴上,点B(12,4),点D(3,0),点E(0,2),过点D作DF⊥DE,交AB于点F,连结EF,将△DEF绕点E逆时针方向旋转,旋转角度为θ(0°<θ<180°).
(1)求tan∠DFE.
(2)在旋转过程中,当△DFE的一边与直线AB平行时,求直线AB截△DFE所得的三角形的面积.
(3)在旋转过程中,当∠DFE的两边所在直线与y轴围成的三角形为等腰三角形时,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录的是今年长江某一周的水位变化情况,这一周的上周末的水位已达到警戒水位33米(正号表示水位比前一天上升,负号表示水位比前一天下降).
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
水位变化(米) |
|
|
|
|
|
|
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句,画出图形并回答问题.
如图,已知三点A,B,C.

(1)分别作直线AB和射线AC;
(2)作线段BC, 取BC的中点D;
(3)连接AD;
(4)用量角器度量出∠ADB的度数最接近( )
A.80° B. 90° C. 100° D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表三行数的规律,回答下列问题:
第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
(1)第1行的第四个数a是 ;第3行的第六个数b是 ;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为 ;
(3)已知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
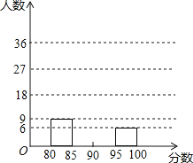
【题目】某校举办“红歌伴我成长”歌咏比赛活动,参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如图:
分数段 | 频数 | 频率 |
80≤x<85 | 9 | 0.15 |
85≤x<90 | m | 0.45 |
90≤x<95 | ■ | ■ |
95≤x<100 | 6 | n |
(1)求m,n的值分别是多少;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水稻种植是嘉兴的传统农业.为了比较甲、乙两种水稻秧苗的长势,农技人员从两块试验田中分别随机抽取5株水稻秧苗,将测得的苗高数据绘制成如图所示的统计图.
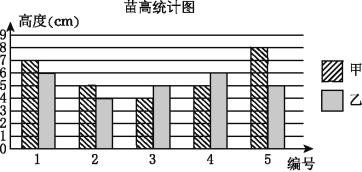
请你根据统计图所提供的数据,计算甲、乙两种水稻苗高的平均数和方差,并比较两种水稻的长势.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com