
【题目】阅读理解:
如图,在平面直角坐标系xOy中,点A与点B的坐标分别是![]() ,
,![]() .
.
![]() 对于坐标平面内的一点P,给出如下定义:如果
对于坐标平面内的一点P,给出如下定义:如果![]() ,则称点P为线段AB的“等角点”
,则称点P为线段AB的“等角点”![]() 显然,线段AB的“等角点”有无数个,且A、B、P三点共圆.
显然,线段AB的“等角点”有无数个,且A、B、P三点共圆.
![]() 设A、B、P三点所在圆的圆心为C,直接写出点C的坐标和
设A、B、P三点所在圆的圆心为C,直接写出点C的坐标和![]() 的半径;
的半径;
![]() 轴正半轴上是否有线段AB的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;
轴正半轴上是否有线段AB的“等角点”?如果有,求出“等角点”的坐标;如果没有,请说明理由;
![]() 当点P在y轴正半轴上运动时,
当点P在y轴正半轴上运动时,![]() 是否有最大值?如果有,说明此时
是否有最大值?如果有,说明此时![]() 最大的理由,并求出点P的坐标;如果没有请说明理由.
最大的理由,并求出点P的坐标;如果没有请说明理由.
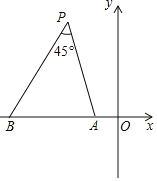
【答案】(1)①![]() 或
或![]() ,半径为
,半径为![]() ,②
,②![]() ,
,![]() .(2)
.(2)![]()
【解析】分析:
(1)①如下图1,连接BC、AC,则由“圆周角定理”可知∠ACB=2∠APB=90°,过点C作CH⊥AB于点H,则由已知条件根据“垂径定理”可得AH=BH=CH=3,从而可得OH=OA+AH=4,由此即可得到点C的坐标为(-4,3)或(-4,-3);此时在Rt△ACH中由勾股定理可求得![]() 的半径为
的半径为![]() ;②如下图2,当点C的坐标为(-4,3)时,过点C作CD⊥y轴于点D,则由CD=4<
;②如下图2,当点C的坐标为(-4,3)时,过点C作CD⊥y轴于点D,则由CD=4<![]() 可知,此时
可知,此时![]() C和y轴有交点,设交点为P1和P2,连接CP1和CP2,利用勾股定理求得DP1和DP2的长度即可求得P1和P2的坐标了;
C和y轴有交点,设交点为P1和P2,连接CP1和CP2,利用勾股定理求得DP1和DP2的长度即可求得P1和P2的坐标了;
(2)如下图3,当过A,B的圆与y轴相切于点P时,∠![]() 最大,设此时圆心为E,则E在第三象限,在y轴的正半轴上任意取一点
最大,设此时圆心为E,则E在第三象限,在y轴的正半轴上任意取一点![]() 不与点P重合
不与点P重合![]() ,连接MA,MB,PA,PB,设MB交
,连接MA,MB,PA,PB,设MB交![]() E于点N,连接NA,则由“圆周角定理”和“三角形外角的性质”易得∠APB=∠ANB>∠AMB,从而说明此时∠APB最大;再过点E作EF⊥x轴于点F,连接EA、EP,易证四边形OPEF是矩形,由此可得PE=OF=4,再Rt△AEF中,由勾股定理可得EF=
E于点N,连接NA,则由“圆周角定理”和“三角形外角的性质”易得∠APB=∠ANB>∠AMB,从而说明此时∠APB最大;再过点E作EF⊥x轴于点F,连接EA、EP,易证四边形OPEF是矩形,由此可得PE=OF=4,再Rt△AEF中,由勾股定理可得EF=![]() ,从而可得OP=
,从而可得OP=![]() ,由此即可得到此时点P的坐标为
,由此即可得到此时点P的坐标为![]() .
.
详解:
(1)①如图1,
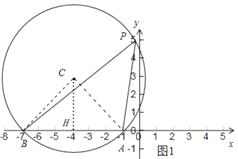
在x轴的上方,作以AB为斜边的直角三角形ACB,易知点A,B,P在![]() 上,连接
上,连接![]() 轴于点H,
轴于点H,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由垂径定理可得,![]() ,
,
∴![]() ,
,![]() ,
,
所以![]() ,半径为
,半径为![]() ,
,
由对称性可知,点![]() 也满足条件.
也满足条件.
②![]() 轴的正半轴上存在线段AB的“等角点”.
轴的正半轴上存在线段AB的“等角点”.
如图2所示,

当圆心为![]() 时,过点C作
时,过点C作![]() 轴于点D,则
轴于点D,则![]() ,
,![]() ,
,
∵![]() 的半径为
的半径为![]() ,
,
∴![]() 与y轴相交,
与y轴相交,
设交点为![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,CA,则
,CA,则![]() ,
,
∵![]() 轴,
轴,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
![]() 当过A,B的圆与y轴相切于点P时,
当过A,B的圆与y轴相切于点P时,![]() 最大.
最大.
理由如下:如果点P在y轴的正半轴上,如图3,
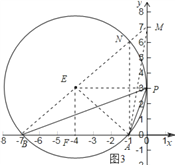
设此时圆心为E,则E在第三象限,在y轴的正半轴上任意取一点![]() 不与点P重合
不与点P重合![]() ,
,
连接MA,MB,PA,PB,设MB交![]() 于点N,连接NA,
于点N,连接NA,
∵点P、点N在![]() 上,
上,
∴![]() ,
,
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,即
,即![]() ,
,
此时,过点E作![]() 轴于点F,连接EA,EP,则
轴于点F,连接EA,EP,则![]() ,
,![]() ,
,
∵![]() 与y轴相切于点P,则
与y轴相切于点P,则![]() 轴,
轴,
∴四边形OPEF是矩形,![]() ,
,![]() ,
,
∴![]() 的半径为4,即
的半径为4,即![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]()


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,某计算器中有![]() 、
、![]() 、
、![]() 三个按键,以下是这三个按键的功能.
三个按键,以下是这三个按键的功能.
①![]() :将荧幕显示的数变成它的算术平方根;②
:将荧幕显示的数变成它的算术平方根;②![]() :将荧幕显示的数变成它的倒数;
:将荧幕显示的数变成它的倒数;
③![]() :将荧幕显示的数变成它的平方.
:将荧幕显示的数变成它的平方.
小明输入一个数据后,按照以下步骤操作,依次按照从第一步到第三步循环按键.
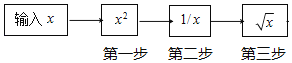
若一开始输入的数据为10,那么第2018步之后,显示的结果是( )

A.![]() B.100C.0.01D.0.1
B.100C.0.01D.0.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC各顶点的坐标分A(-2,-2),B(-4,-1),C(-4,-4).

(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在
△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中
①一个角的两边分别垂直于另一角的两边,则这两个角相等或互补
②若点A在y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一象限
③半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的共有四个
④如果AD是△ABC的高,∠CAD=∠B,那么△ABC是直角三角形
正确命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为打造智慧课堂,准备集体购买一批平板电脑,原计划订购60台,每台1000元,商家表示,如果多购,可以优惠,结果校长实际订购了72台,每台减价30元,但商家获得同样多的利润.
(1)求每台平板电脑的成本是多少元?
(2)求商家的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
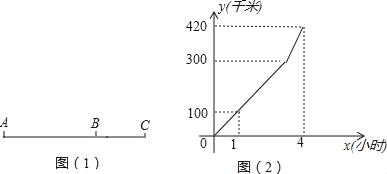
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句,画出图形并回答问题.
如图,已知三点A,B,C.

(1)分别作直线AB和射线AC;
(2)作线段BC, 取BC的中点D;
(3)连接AD;
(4)用量角器度量出∠ADB的度数最接近( )
A.80° B. 90° C. 100° D. 110°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com