
阅读理【解析】
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
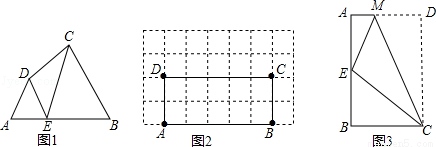
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
科目:初中数学 来源:2016届山东省泰安市东平县九年级上学期期中数学试卷(解析版) 题型:选择题
如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
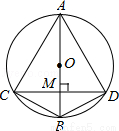
A.CM=DM B. =
= C.∠ACD=∠ADC D.OM=MD
C.∠ACD=∠ADC D.OM=MD
查看答案和解析>>
科目:初中数学 来源:2016届山东省青岛市黄岛区九年级上学期期中数学试卷(解析版) 题型:选择题
一个矩形的两条对角线的一个夹角为60°,对角线长为10,则这个矩形的面积为( )
A.25 B.50 C.25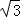 D.50
D.50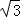
查看答案和解析>>
科目:初中数学 来源:2016届山东省九年级上学期10月月考数学试卷(解析版) 题型:选择题
若菱形两条对角线的长分别为6和8,则这个菱形的周长为( )
A.20 B.16 C.12 D.10
查看答案和解析>>
科目:初中数学 来源:2016届江苏省扬州市九年级上学期11月月考数学试卷(解析版) 题型:解答题
如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.
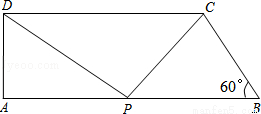
(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2016届江苏省扬州市九年级上学期11月月考数学试卷(解析版) 题型:填空题
如图,已知△ABC是面积为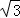 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
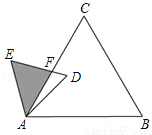
查看答案和解析>>
科目:初中数学 来源:2016届江苏省九年级下学期第一次月考数学试卷(解析版) 题型:解答题
2013年我国多地出现雾霾天气,某企业抓住商机准备生产空气净化设备,该企业决定从以下两个投资方案中选择一个进行投资生产,方案一:生产甲产品,每件产品成本为a元(a为常数,且40<a<100),每件产品销售价为120元,每年最多可生产125万件;方案二:生产乙产品,每件产品成本价为80元,每件产品销售价为180元,每年可生产120万件,另外,年销售x万件乙产品时需上交0.5x2万元的特别关税,在不考虑其它因素的情况下:
(1)分别写出该企业两个投资方案的年利润y1(万元)、y2(万元)与相应生产件数x(万件)(x为正整数)之间的函数关系式,并指出自变量的取值范围;
(2)分别求出这两个投资方案的最大年利润;
(3)如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com