
【题目】解不等式和不等式组:
(1)x为何值时,代数式 ![]() 的值比
的值比 ![]() 的值大1.
的值大1.
(2)解不等式组: ![]() ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
【答案】
(1)解:根据题意,得: ![]() ﹣
﹣ ![]() =1,
=1,
∴2(x+4)﹣3(3x﹣1)=6,
2x+8﹣9x+3=6,
2x﹣9x=6﹣8﹣3,
﹣7x=﹣5,
∴x= ![]()
(2)解:解不等式①,得:x≤3,
解不等式②,得:x>﹣1,
∴不等式组的解集为﹣1<x≤3,
将解集表示在数轴上如下:
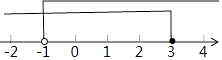
【解析】(1)根据题意列出方程,在依据解一元一次方程的基本步骤依次进行可得答案;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【考点精析】通过灵活运用解一元一次方程的步骤和不等式的解集在数轴上的表示,掌握先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈即可以解答此题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
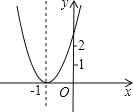
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
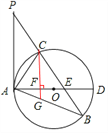
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AGAB=48,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=2,求⊙O的半径及sin∠ACE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算。
(1)你发现了吗?( ![]() )2=
)2= ![]() ×
× ![]() ,(
,( ![]() )﹣2=
)﹣2= ![]() =
= ![]() ×
× ![]() =
= ![]() ×
× ![]() 由上述计算,我们发现(
由上述计算,我们发现( ![]() )2(
)2( ![]() )﹣2;
)﹣2;
(2)仿照(1),请你通过计算,判断( ![]() )3与(
)3与( ![]() )﹣3之间的关系.
)﹣3之间的关系.
(3)我们可以发现:( ![]() )﹣m(
)﹣m( ![]() )m(ab≠0)
)m(ab≠0)
(4)计算:( ![]() )﹣4×(
)﹣4×( ![]() )4 .
)4 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠ACB=90°,∠A=30°,DE垂直平分AC,D为垂足,交AB于E,连接CE. 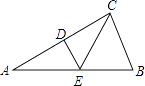
(1)求∠ECB的度数;
(2)若AB=10,求△BCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P在第二象限,且到两条坐标轴的距离都是4,则点P的坐标为( )
A. (﹣4,4) B. (﹣4,﹣4) C. (4,﹣4) D. (4,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC, ①如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+ ![]() ∠A;
∠A;
②如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°﹣∠A;
③如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°﹣ ![]() ∠A.
∠A.
上述说法正确的个数是( )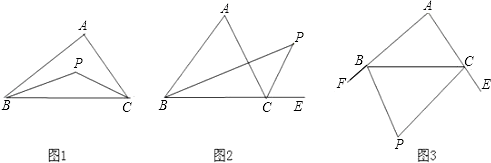
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com