
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)填空:点A的坐标: ;点B的坐标: ;
(2)若CD平分∠ACO,交x轴于D,求点D的坐标;
(3)在(2)的条件下,经过点D的直线交直线BC于E,当△CDE为以CD为底的等腰三角形时,求点E的坐标.

【答案】(1)(12,0),(12,9);(2)D(![]() ,0);(3)E(
,0);(3)E(![]() ,9).
,9).
【解析】
(1)根据矩形的性质即可解决问题;
(2)如图1中,作DM⊥AC于M.由Rt△CDO≌Rt△CDM(HL),推出CM=OC=9,由AC=![]() =15,推出AM=6,设OD=DM=m,在Rt△ADM中,根据AD2=DM2+AM2,构建方程即可解决问题;
=15,推出AM=6,设OD=DM=m,在Rt△ADM中,根据AD2=DM2+AM2,构建方程即可解决问题;
(3)如图2中,作线段CD的中垂线EF,垂足为F,交BC 于E,则EC=ED,△ECD是以CD为底的等腰三角形.想办法求出直线EF的解析式即可解决问题;
解:(1)∵四边形OABC是矩形,
∴AB=OC=9,BC=OA=12,
∴A(12,0),B(12,9),
故答案为(12,0),(12,9);
(2)如图1中,作DM⊥AC于M.
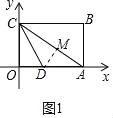
∵DC平分∠ACO,DO⊥CO,DM⊥AC,
∴DO=DM,∠COD=∠CMD=90°,
∵CD=CD,
∴Rt△CDO≌△Rt△CDM(HL),
∴CM=OC=9,
∵AC=![]() =15,
=15,
∴AM=6,设OD=DM=m,
在Rt△ADM中,∵AD2=DM2+AM2,
∴x2+62=(12﹣x)2,
解得x=![]() ,
,
∴D(![]() ,0).
,0).
(3)如图2中,作线段CD的中垂线EF,垂足为F,交BC 于E,则EC=ED,△ECD是以CD为底的等腰三角形.
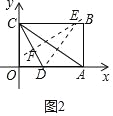
∵C(0,9),D(![]() ,0),
,0),
∴直线CD的解析式为y=﹣2x+9,
∴F(![]() ,
,![]() ),
),
∴直线EF的解析式为y=![]() x+
x+![]() ,
,
当y=9时,x=![]() ,
,
∴E(![]() ,9).
,9).


科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,且与OA交于点E,与OB交于点F,连接CE,CF. 
(1)求证:AB与⊙O相切.
(2)若∠AOB=∠ECF,试判断四边形OECF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
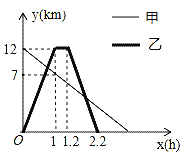
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海滨浴场东西走向的海岸线可近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号.他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲、乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的仰角∠EAB为15°,码头D的仰角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)设方程两根为x1 , x2是否存在实数a,使 ![]() ?若存在求出实数a,若不存在,请说明理由.
?若存在求出实数a,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E.下列结论错误的是( )
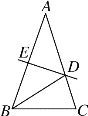
A. BD平分∠ABC B. △BCD的周长等于AB+BC
C. AD=BD=BC D. 点D是线段AC的中点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com