
【题目】如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(﹣3,5),C(﹣4,1).
①把△ABC向右平移2个单位得△A1B1C1 , 请画出△A1B1C1 , 并写出点A1的坐标;
②把△ABC绕原点O旋转180°得到△A2B2C2 , 请画出△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1 , 画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2 .
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l:y= ![]() x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A5B6A6的周长是( )
x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A5B6A6的周长是( )
A.24 ![]()
B.48 ![]()
C.96 ![]()
D.192 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),并与y= ![]() 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
(1)求一次函数与反比例函数的解析式;
(2)若点C′是点C关于y轴的对称点,请求出△ABC′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
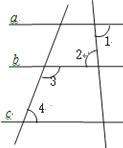
解:a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,OA=12,OC=9,连接AC.
(1)填空:点A的坐标: ;点B的坐标: ;
(2)若CD平分∠ACO,交x轴于D,求点D的坐标;
(3)在(2)的条件下,经过点D的直线交直线BC于E,当△CDE为以CD为底的等腰三角形时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系内,画在透明胶片上的ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(5,﹣1)处,则此平移可以是( )
A.先向右平移5个单位,再向下平移1个单位
B.先向右平移5个单位,再向下平移3个单位
C.先向右平移4个单位,再向下平移1个单位
D.先向右平移4个单位,再向下平移3个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com