
【题目】如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),并与y= ![]() 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
(1)求一次函数与反比例函数的解析式;
(2)若点C′是点C关于y轴的对称点,请求出△ABC′的面积.
【答案】
(1)
解:∵直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),
∴ ![]() ,
,
解得 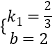 .
.
∴一次函数的解析式为y= ![]() x+2.
x+2.
∵OB是△ACD的中位线,OA=3,OB=2,∴OD=3,DC=4.
∴C(3,4).
∵点C在双曲线y= ![]() 上,
上,
∴k2=3×4=12.
∴反比例函数的解析式为y= ![]() .
.
(2)
解:∵点C′是点C(3,4)关于y轴的对称点,
∴C′(﹣3,4).
∴AC′⊥AO.
∴S△ABC′=S梯形AOBC′﹣S△ABO= ![]() (2+4)×3﹣
(2+4)×3﹣ ![]() 3×2=6.
3×2=6.
【解析】(1)根据直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),代入解析式,求出k1和b的值,从而得出一次函数的解析式;再根据OB是△ACD的中位线,得出点C的坐标,最后代入双曲线y= ![]() ,即可求出反比例函数的解析式.(2)根据点C′是点C(3,4)关于y轴的对称点,求出C′的坐标,从而得出AC′⊥AO,最后根据S△ABC′=S梯形AOBC′﹣S△ABO , 代入计算即可.
,即可求出反比例函数的解析式.(2)根据点C′是点C(3,4)关于y轴的对称点,求出C′的坐标,从而得出AC′⊥AO,最后根据S△ABC′=S梯形AOBC′﹣S△ABO , 代入计算即可.


科目:初中数学 来源: 题型:
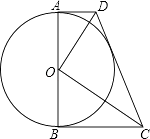
【题目】如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC= ![]() .
. 
(1)求OD、OC的长;
(2)求证:△DOC∽△OBC;
(3)求证:CD是⊙O切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF .
其中,将正确结论的序号全部选对的是( )
A.①②③
B.①②④
C.②③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,且与OA交于点E,与OB交于点F,连接CE,CF. 
(1)求证:AB与⊙O相切.
(2)若∠AOB=∠ECF,试判断四边形OECF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′,则点B在旋转过程中所经过的路线的长是cm.(结果保留π)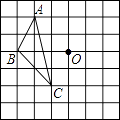
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
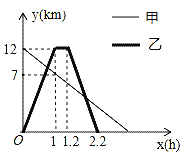
【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的仰角∠EAB为15°,码头D的仰角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程:
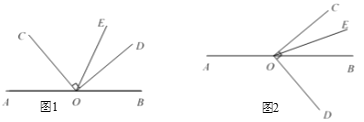
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =![]() ∠BOC ( ).
∠BOC ( ).
∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com