
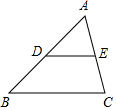
 如图,在△ABC中,点D,E分别是边AB,AC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,在△ABC中,点D,E分别是边AB,AC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.分析 (1)首先利用平面向量三角形法则求得$\overrightarrow{AC}$,然后由“E是边AC的中点”来求向量$\overrightarrow{CE}$;
(2)利用平行四边形法则,即可求得向量$\overrightarrow{BA}$,$\overrightarrow{BC}$方向上的分向量.
解答 解:(1)∵在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
∴$\overrightarrow{AC}$=$\overrightarrow{AB}$-$\overrightarrow{BC}$=$\overrightarrow{a}$-=$\overrightarrow{b}$.
又∵E是边AC的中点,
∴$\overrightarrow{CE}$=$\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$.
故答案是:$\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$;
(2)如图,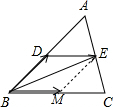
过点E作EM∥AB交BC于点M.
$\overrightarrow{BD}$、$\overrightarrow{BM}$即为向量$\overrightarrow{BE}$在向量$\overrightarrow{BA}$,$\overrightarrow{BC}$方向上的分向量.
点评 此题考查了平面向量的知识.此题比较简单,注意掌握三角形法则与平行四边形法则的应用.


科目:初中数学 来源: 题型:选择题
| A. | 无意义 | B. | 有意义 | C. | 值为0 | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | tanB=$\frac{2}{3}$ | B. | cotB=$\frac{2}{3}$ | C. | sinB=$\frac{2}{3}$ | D. | cosB=$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |${\overrightarrow b}$|=2|$\overrightarrow a}$| | B. | 2$\overrightarrow a+\overrightarrow b=0$ | C. | $\overrightarrow b∥\overrightarrow a$ | D. | $\overrightarrow b≠\overrightarrow a$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
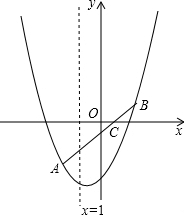 如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.
如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com