
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
【答案】(1)3,12;(2)D(![]() ,3);(3)
,3);(3)![]() 或
或![]() .
.
【解析】试题分析:(1)把点A(4,n)代入一次函数y=![]() x-3,得到n的值为3;再把点A(4,3)代入反比例函数
x-3,得到n的值为3;再把点A(4,3)代入反比例函数![]() ,得到k的值为12;
,得到k的值为12;
(2)根据坐标轴上点的坐标特征可得点B的坐标为(2,0),过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,根据勾股定理得到AB=![]() ,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
(3)根据反比函数的性质即可得到当y≥-2时,自变量x的取值范围.
试题解析:(1)把点A(4,n)代入一次函数y=![]() x-3,可得n=
x-3,可得n=![]() ×4-3=3;
×4-3=3;
把点A(4,3)代入反比例函数![]() ,可得3=
,可得3=![]() ,
,
解得k=12.
(2)∵一次函数y=![]() x-3与x轴相交于点B,
x-3与x轴相交于点B,
∴![]() x-3=0,
x-3=0,
解得x=2,
∴点B的坐标为(2,0),
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,
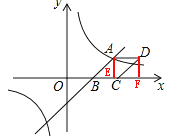
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OE-OB=4-2=2,
在Rt△ABE中,
AB=![]() ,
,
∵四边形ABCD是菱形,
∴AB=CD=BC=![]() ,AB∥CD,
,AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
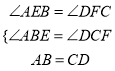 ,
,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+![]() +2=4+
+2=4+![]() ,
,
∴点D的坐标为(4+![]() ,3).
,3).
(3)当y=-2时,-2=![]() ,解得x=-6.
,解得x=-6.
故当y≥-2时,自变量x的取值范围是x≤-6或x>0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商品原价800元,连续两次降价a%后售价为578元,下列所列方程正确的是( )
A.800(1+a%)2=578
B.800(1﹣a%)2=578
C.800(1﹣2a%)=578
D.800(1﹣a2%)=578
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果顺次连接一个四边形各边中点所得新的四边形是菱形,那么对这个四边形的形状描述最准确的是( )
A.矩形B.等腰梯形C.菱形D.对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生利用双休时间去距学校20km的白水寺参观,一部分学生骑自行车先走,过了40min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,骑车学生的速度是_____________Km/h.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )
A.(2,5)
B.(5,2)
C.(4, ![]() )
)
D.( ![]() ,4)
,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com