17.下列各代数式中,是分式的有$\frac{1}{x}$,$\frac{4}{{a}^{2}-5}$,$\frac{2a}{{x}^{2}y}$,$\frac{1}{5}x-\frac{z}{y}$
$\frac{x}{2}$,$\frac{1}{x}$,$\frac{4}{{a}^{2}-5}$,$\frac{2}{π}$,$\frac{2a}{{x}^{2}y}$,$\frac{1}{5}x-\frac{z}{y}$,-2a.
分析 判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
解答 解:$\frac{1}{x}$,$\frac{4}{{a}^{2}-5}$,$\frac{2a}{{x}^{2}y}$,$\frac{1}{5}x-\frac{z}{y}$是分式,
故答案为:$\frac{1}{x}$,$\frac{4}{{a}^{2}-5}$,$\frac{2a}{{x}^{2}y}$,$\frac{1}{5}x-\frac{z}{y}$.
点评 本题主要考查分式的定义,注意π不是字母,是常数,所以$\frac{2}{π}$不是分式,是整式.

 名校课堂系列答案
名校课堂系列答案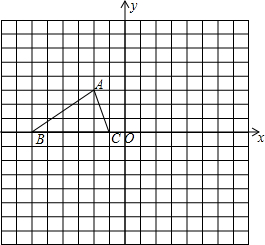 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).