
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG.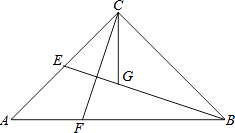
(1)求证:CF=BG;
(2)延长CG交AB于点H,判断点G是否在线段AB的垂直平分线上?并说明理由.
(3)过点A作AD⊥AB交BE的延长线于点D,请证明:CF=2DE.
【答案】
(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∵CG平分∠ACB,
∴∠BCG=45°=∠A,
∴∠BCG=∠CAB=45°,
在△ACF和△BCG中, 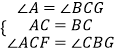 ,
,
∴△ACF≌△BCG(ASA),
∴AF=CG,CF=BG
(2)解:点G在线段AB的垂直平分线上,如图1所示:理由如下:

∵AC=BC,CG平分∠ACB,
∴CH⊥AB,H为AB中点,
∴点G在线段AB的垂直平分线上
(3)证明:连接AG.如图2所示:
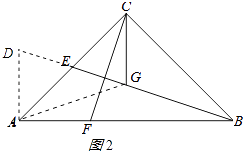
由(2)可知,AG=BG,∠GAB=∠GBA,
∵AD⊥AB,
∴∠GAB+∠GAD=∠GBA+∠D=90°,
∴∠GAD=∠D,
∴GA=GD=GB=CF.
∵AD⊥AB,CH⊥AB
∴CH∥AD,
∴∠D=∠EGC,
∵E为AC中点,
∴AE=EC,
在△AED和△CEG中, 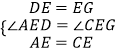 ,
,
∴△AED≌△CEG(SAS),
∴DE=EG,
∴DG=2DE,
∴CF=2DE
【解析】(1)根据角平分线的性质、等边对等角和已知条件证明出△ACF≌△BCG,得出AF=CG,CF=BG;(2)根据等腰三角形的三线合一,得到点G在线段AB的垂直平分线上;(3)由(2)可知,AG=BG,∠GAB=∠GBA,已知AD⊥AB,得到∠GAD=∠D,GA=GD=GB=CF,得到 △AED≌△CEG,得到DE=EG,DG=2DE,CF=2DE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
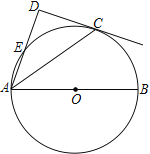
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC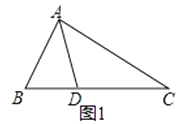
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)…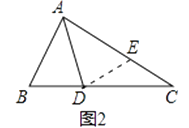
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE. 可以证得:AE=DE(如图3)…
请你任意选择一种思路继续完成下一步的证明.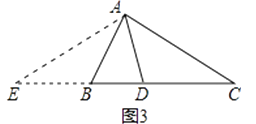
(2)【变式探究】
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4),AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.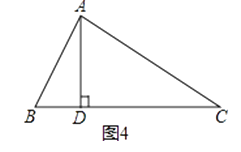
(3)【迁移拓展】
△ABC中,∠B=2∠C. 求证:AC2=AB2+ABBC. (如图5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
【问题情境】金老师给“数学小达人”小明和小军提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC.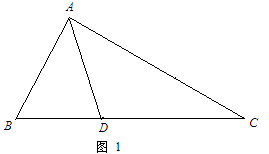
【证明思路】小明的证明思路是:如图2,在AC上截取AE=AB,连接DE.……
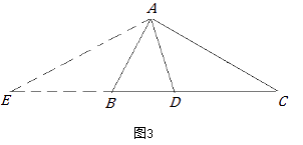
小军的证明思路是:如图3,延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE.……
(1)请你从他们的思路中,任意选择一种思路继续完成下一步的证明.
(2)【变式探究】如图4,金老师把“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变,那么AB+BD=AC还成立吗?若成立,请证明;若不成立,写出正确结论,并说明理由.
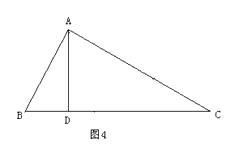
(3)【迁移拓展】如图5,△ABC中,∠B=2∠C.求证:AC2—AB2=AB×BC.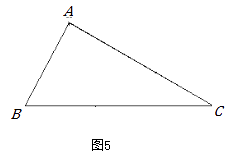
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店某天销售了14件衬衫,其领口尺寸统计如表:
领口尺寸(单位:cm) | 38 | 39 | 40 | 41 | 42 |
件数 | 1 | 5 | 3 | 3 | 2 |
则这14件衬衫领口尺寸的众数与中位数分别是( )
A.39cm、39cm
B.39cm、39.5cm
C.39cm、40cm
D.40cm、40cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),
图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),![]() 是抛物线上两点,则y1>y2,其中说法正确的有( )
是抛物线上两点,则y1>y2,其中说法正确的有( )
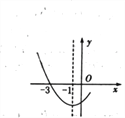
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com