
【题目】综合题
(1)【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC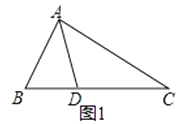
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)…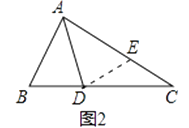
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE. 可以证得:AE=DE(如图3)…
请你任意选择一种思路继续完成下一步的证明.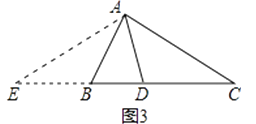
(2)【变式探究】
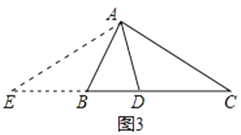
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4),AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.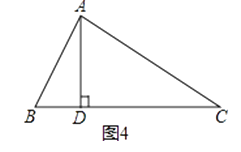
(3)【迁移拓展】
△ABC中,∠B=2∠C. 求证:AC2=AB2+ABBC. (如图5)
【答案】
(1)解:小敏的证明思路是:如图2,在AC上截取AE=AB,连接DE.(如图2)
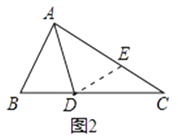
∵AD是∠BAC的平分线,
∴∠BAD=∠EAD.
在△ABD和△AED中,
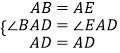 ,
,
∴△ABD≌△AED(SAS),
∴BD=DE,∠ABD=∠AED
∵∠AED=∠EDC+∠C,∠B=2∠C,
∴∠EDC=∠C,
∴DE=EC,
即AB+BD=AC;
小捷的证明思路是:如图3,延长CB至点E,使BE=AB,连接AE.
∴∠E=∠BAE.
∵∠ABC=∠E+∠BAE,
∴∠ABC=2∠E.
∵∠ABC=2∠C,
∴∠E=∠C,
∴△AEC是等腰三角形.
∵AD是∠BAC的平分线,
∴∠BAD=∠DAC.
∵∠ADE=∠DAC+∠C,∠DAE=∠BAD+∠BAE
∴∠ADE=∠DAE,
∴EA=ED=AC,
∴AB+BD=AC
(2)解:AB+BD=AC不成立 正确结论:AB+BD=CD
理由:如图4,在CD上截取DE=DB,连结AE,
∵AD⊥BC,
∴AD是BE的中垂线,
∴AE=AB,
∴∠B=∠AED.
∵∠AED=∠C+∠CAE,且∠B=2∠C,
∴∠C=∠CAE,
∴AE=EC.
即AB+BD=CD
(3)解:证明:如图5,过点A作AD⊥BC于D.
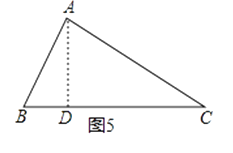
由勾股定理得:AB2=BD2+AD2,AC2=CD2+AD2,
∴AC2﹣AB2=CD2﹣BD2=(CD+BD)(CD﹣BD)=BC(CD﹣BD)
∵AB+BD=CD,
∴CD﹣BD=AB,
∴AC2﹣AB2=BC(CD﹣BD)=BCAB,
即AC2=AB2+ABBC
【解析】【问题情境】小敏的证明思路是:在AC上截取AE=AB,由角平分线的性质就可以得出∠DAB=∠DAE,再证明△ADB≌ADE就可以得出结论;小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.就可以得出∠E=∠C,就有AE=AC,进而得出AE=ED即可;
【变式探究】CD上截取DE=DB,连结AE,由AD⊥BC就可以得出AE=AB,∠AED=∠B,由∠AED=∠C+∠CAE就有∠C=∠CAE得出AE=EC,进而得出结论;
【迁移拓展】过点A作AD⊥BC于D.由勾股定理得:AB2=BD2+AD2,AC2=CD2+AD2,AC2-AB2=CD2-BD2=BC(CD-BD),由(2)的结论就可以得出AC2-AB2=BC(CD-BD)=BCAB即可.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,已知1号、4号两个正方形的面积和为10, 2号、3号两个正方形的面积和为7,则a,b,c三个方形的面积和为( )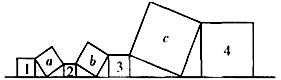
A.17
B.27
C.24
D.34
查看答案和解析>>
科目:初中数学 来源: 题型:
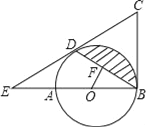
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=﹣ ![]() x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.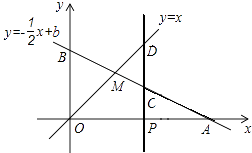
(1)求点A的坐标;
(2)在x轴上有一点动点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣ ![]() x+b和y=x的图象于点C、D,且OB=2CD,求a的值.
x+b和y=x的图象于点C、D,且OB=2CD,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )
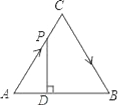
A.  B.
B.  C.
C. 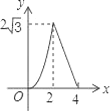 D.
D. 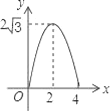
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C.
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)求证:AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将等腰直角△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(-2,1).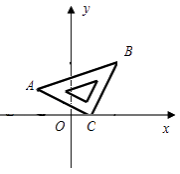
(1)求△ABC的面积S;
(2)求直线AB与y轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG.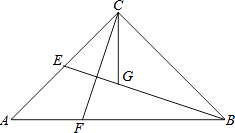
(1)求证:CF=BG;
(2)延长CG交AB于点H,判断点G是否在线段AB的垂直平分线上?并说明理由.
(3)过点A作AD⊥AB交BE的延长线于点D,请证明:CF=2DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣6x2可以看作是由抛物线y=﹣6x2+5按下列何种变换得到( )
A.向上平移5个单位
B.向下平移5个单位
C.向左平移5个单位
D.向右平移5个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com