
【题目】如图,已知函数y=﹣ ![]() x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.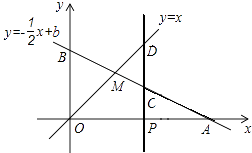
(1)求点A的坐标;
(2)在x轴上有一点动点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣ ![]() x+b和y=x的图象于点C、D,且OB=2CD,求a的值.
x+b和y=x的图象于点C、D,且OB=2CD,求a的值.
【答案】
(1)解:∵点M在函数y=x的图象上,且横坐标为2,
∴点M的纵坐标为2.
∵点M(2,2)在一次函数y=﹣ ![]() x+b的图象上,(1)首先求出M点的坐标,然后再将M点的坐标代入y=﹣
x+b的图象上,(1)首先求出M点的坐标,然后再将M点的坐标代入y=﹣ ![]() x+b求出b的值,得到解析式,最后求出A点的坐标;
x+b求出b的值,得到解析式,最后求出A点的坐标;
∴﹣ ![]() ×2+b=2,
×2+b=2,
∴b=3,
∴一次函数的表达式为y=﹣ ![]() x+3,令y=0,得x=6,
x+3,令y=0,得x=6,
∴点A的坐标为(6,0)
(2)解:由题意得:C(a,﹣ ![]() a+3),D(a,a),
a+3),D(a,a),
∴CD=a﹣(﹣ ![]() a+3).
a+3).
∵OB=2CD,
∴a﹣(﹣ ![]() a+3)=
a+3)= ![]() ,
,
∴a=3
【解析】(1)首先求出M点的坐标,然后再将M点的坐标代入y=﹣ ![]() x+b求出b的值,得到解析式,最后求出A点的坐标;
x+b求出b的值,得到解析式,最后求出A点的坐标;
(2)根据平行于y轴的直线上的点的横坐标相同,由P点的坐标表示出C,D两点的坐标,进而表示出CD的长,根据OB=2CD,列出方程,求出a的值。


科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
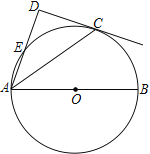
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年度中央机关及其直属机构公务员招考网上报名已经结束,据初步统计,网上报名人数约有211.5万人,数据211.5万用科学记数法可表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC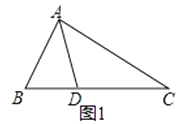
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)…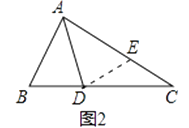
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE. 可以证得:AE=DE(如图3)…
请你任意选择一种思路继续完成下一步的证明.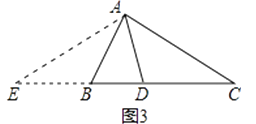
(2)【变式探究】
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4),AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.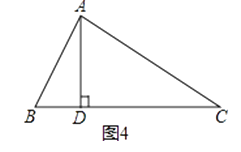
(3)【迁移拓展】
△ABC中,∠B=2∠C. 求证:AC2=AB2+ABBC. (如图5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),
图像的一部分,其对称轴为x=-l,且过点(-3,0).下列说法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),![]() 是抛物线上两点,则y1>y2,其中说法正确的有( )
是抛物线上两点,则y1>y2,其中说法正确的有( )
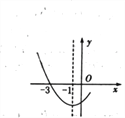
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com