
【题目】将等腰直角△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(-2,1).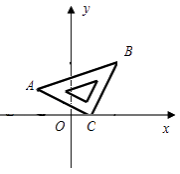
(1)求△ABC的面积S;
(2)求直线AB与y轴的交点坐标.
【答案】
(1)解:过点A作AD⊥x轴,垂足为D.

则AD=1,CD=3, ∴ ![]() ,S=
,S= ![]() =5
=5
(2)解:过点B作BE⊥x轴,垂足为E,
∴∠ADC=∠CEB=90°,则∠CAD+ ∠ACD=90°,
∴∠ACB=90°,则∠BCE+ ∠ACD=90°, ∴∠CAD=∠BCE,
又∵∠ADC=∠CEB=90°,AC=BC,
∴△ADC≌△CEB, ∴CD=BE=3,CE=AD=1,
∴点B的坐标为(2,3).
设直线AB的解析式为y=kx+b,则 ![]() ,
,
解得: ![]() ,
,
所以y= ![]() x+2,
x+2,
所以直线AB交y轴于点(0,2)
【解析】(1)根据题意和勾股定理求出AD、CD、AC2的值,得到△ABC的面积;(2)根据题意得到△ADC≌△CEB, CD=BE,CE=AD的值,求出点B的坐标,用待定系数法把A、B的坐标代入,求出直线AB的解析式,求出直线AB与y轴的交点坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为解决“最后一公里一的交通接驳同题,苏州市投放了大量公租自行车供 市民使用到2014年底,全市已有公租自行车25 000辆,租赁点600个,预计到2016年底,全市将有公租自行车50 000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC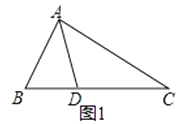
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)…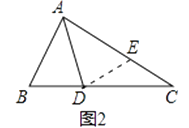
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE. 可以证得:AE=DE(如图3)…
请你任意选择一种思路继续完成下一步的证明.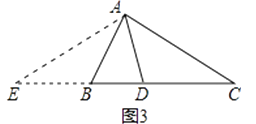
(2)【变式探究】
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4),AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.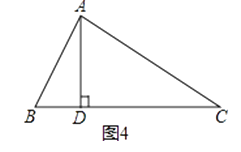
(3)【迁移拓展】
△ABC中,∠B=2∠C. 求证:AC2=AB2+ABBC. (如图5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店某天销售了14件衬衫,其领口尺寸统计如表:
领口尺寸(单位:cm) | 38 | 39 | 40 | 41 | 42 |
件数 | 1 | 5 | 3 | 3 | 2 |
则这14件衬衫领口尺寸的众数与中位数分别是( )
A.39cm、39cm
B.39cm、39.5cm
C.39cm、40cm
D.40cm、40cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com