
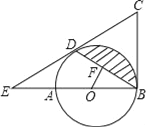
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)首先连接OD,由BC是⊙O的切线,可得∠ABC=90°,又由CD=CB,OB=OD,易证得∠ODC=∠ABC=90°,即可证得CD为⊙O的切线;
(2)在Rt△OBF中,∠ABD=30°,OF=1,可求得BD的长,∠BOD的度数,又由S阴影=S扇形OBD-S△BOD,即可求得答案.
试题解析:(1)连接OD,
∵BC是⊙O的切线,
∴∠ABC=90°,
∵CD=CB,
∴∠CBD=∠CDB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODC=∠ABC=90°,
即OD⊥CD,
∵点D在⊙O上,
∴CD为⊙O的切线;
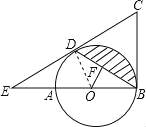
(2)过点O作OF⊥BD于点F,
在Rt△OBF中,
∵∠ABD=30°,OF=1,
∴∠BOF=60°,OB=2,BF=![]() ,
,
∵OF⊥BD,
∴BD=2BF=2![]() ,∠BOD=2∠BOF=120°,
,∠BOD=2∠BOF=120°,
∴S阴影=S扇形OBD﹣S△BOD=![]() ﹣
﹣![]() ×2
×2![]() ×1=
×1=![]() π﹣
π﹣![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】净水机的核心部件就是水处理反渗透膜,水处理反渗透膜就像是一个筛子,它的孔径只有0.11纳米,水在压力的作用下一层层过滤,离子以上的杂质像抗生素、重金属、细菌等都能过滤掉,0.11纳米即0.00000000011米,将0.11纳米用科学记数法表示为( )
A.1.1×10﹣9米
B.1.1×10﹣10米
C.11×10﹣9米
D.0.11×10﹣9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决“最后一公里一的交通接驳同题,苏州市投放了大量公租自行车供 市民使用到2014年底,全市已有公租自行车25 000辆,租赁点600个,预计到2016年底,全市将有公租自行车50 000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
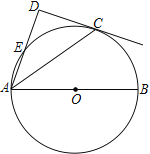
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为![]()
(1)试求袋中绿球的个数;

(2)第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年度中央机关及其直属机构公务员招考网上报名已经结束,据初步统计,网上报名人数约有211.5万人,数据211.5万用科学记数法可表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC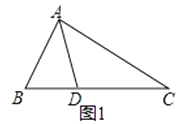
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)…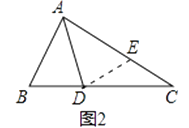
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE. 可以证得:AE=DE(如图3)…
请你任意选择一种思路继续完成下一步的证明.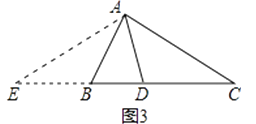
(2)【变式探究】
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4),AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.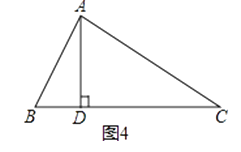
(3)【迁移拓展】
△ABC中,∠B=2∠C. 求证:AC2=AB2+ABBC. (如图5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店某天销售了14件衬衫,其领口尺寸统计如表:
领口尺寸(单位:cm) | 38 | 39 | 40 | 41 | 42 |
件数 | 1 | 5 | 3 | 3 | 2 |
则这14件衬衫领口尺寸的众数与中位数分别是( )
A.39cm、39cm
B.39cm、39.5cm
C.39cm、40cm
D.40cm、40cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com