
 如图,已知C是线段AB上的一点,M,N分别是AC,BC的中点.
如图,已知C是线段AB上的一点,M,N分别是AC,BC的中点.分析 (1)根据M、N分别是AC、BC的中点,可得MC=AM=$\frac{1}{2}$AC,CN=BN=$\frac{1}{2}$BC,即可得到MN=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB;
(2)方法同(1);
(3)根据(1)(2)的结论即可得到结果;
(4)方法同(1).
解答 解:∵M、N分别是AC、BC的中点,
∴MC=AM=$\frac{1}{2}$AC,CN=BN=$\frac{1}{2}$BC,
∴MN=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB=9cm;
(2)由(1)证得MN=$\frac{1}{2}$AB=9cm;
(3)根据(1)(2),发现MN=$\frac{1}{2}$AB;
(4)由(1)证得MN=$\frac{1}{2}$AB=$\frac{1}{2}$a(cm).
点评 本题考查了两点间的距离,熟练掌握线段中点的性质是解题关键.


科目:初中数学 来源: 题型:解答题
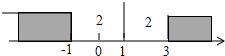 阅读下面材料:
阅读下面材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点M是AB的中点,点N是BD的中点,AB=$\frac{2}{3}$BC,且BC=12cm,CD=6cm.
如图,点M是AB的中点,点N是BD的中点,AB=$\frac{2}{3}$BC,且BC=12cm,CD=6cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
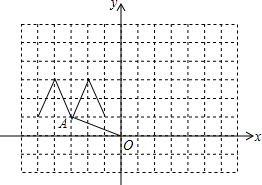 数学的英语单词为mathematical,画出第一个大写字母M绕着原点顺时针旋转90°,180°,270°后的图形,并计算出OA点所在运动的过程扫过的面积.
数学的英语单词为mathematical,画出第一个大写字母M绕着原点顺时针旋转90°,180°,270°后的图形,并计算出OA点所在运动的过程扫过的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
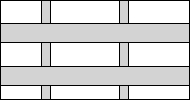 如图,要设计一副宽20cm,长30cm的图象,其中两幅两竖的彩条,横竖彩条的宽度比为2:1,如果要使彩条所占面积是图案面积是$\frac{19}{75}$,那么竖彩条宽度为多少?
如图,要设计一副宽20cm,长30cm的图象,其中两幅两竖的彩条,横竖彩条的宽度比为2:1,如果要使彩条所占面积是图案面积是$\frac{19}{75}$,那么竖彩条宽度为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一艘巡洋舰从点A出发,沿正南方向航行了半小时到达点B,再沿南偏西60°方向航行了半小时到达点C,此时测得码头D在C的正东方向,该巡洋舰的速度为80海里/时.
如图,一艘巡洋舰从点A出发,沿正南方向航行了半小时到达点B,再沿南偏西60°方向航行了半小时到达点C,此时测得码头D在C的正东方向,该巡洋舰的速度为80海里/时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com