Question

14．数学的英语单词为mathematical，画出第一个大写字母M绕着原点顺时针旋转90°，180°，270°后的图形，并计算出OA点所在运动的过程扫过的面积．

Answer 1

分析 利用网格特点和旋转的性质，分别画出大写字母M绕着原点顺时针旋转90°，180°，270°后5个顶点的对应点的位置，从而得到旋转的图形，然后根据扇形面积公式计算OA所扫过的面积．

解答 解：如图，大写字母M绕着原点顺时针旋转90°，180°，270°后的图形如图所示，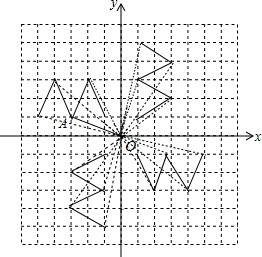

OA=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
所以OA在运动的过程中扫过的面积=$\frac{270•π•（\sqrt{10}）^{2}}{360}$=$\frac{15}{2}$π．

点评 本题考查了作图-旋转：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了扇形的面积公式．