
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
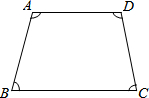 多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.
多边形的内角和随着边数的变化而变化.设多边形的边数为n,内角和为N,则变量N与n之间的关系可以表示为N=(n-2)•180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
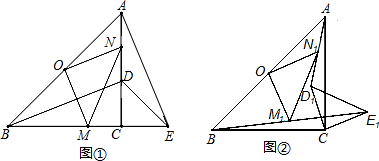
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 200 | |
| B. | 被抽取的200名学生 | |
| C. | 被抽取的200名考生的段考数学成绩 | |
| D. | 某校七年级段考数学成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | π | B. | $\frac{1}{5}$ | C. | $\sqrt{4}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com