
【题目】某班级同学从学校出发去太阳岛研学旅行,一部分乘坐大客车先出发,余下的同学20min后乘坐小轿车沿同一路线出行,大客车中途停车等候5min,小轿车赶上来之后,大客车以出发时速度的![]() 继续行驶,小轿车保持原速度不变.小轿车司机因路线不熟错过了景点入口,在驶过景点入口6 km时,原路提速返回,恰好与大客车同时到达景点入口.两车距学校的路程S(单位:km)和行驶时间t(单位:min)之间的函数关系如图所示.
继续行驶,小轿车保持原速度不变.小轿车司机因路线不熟错过了景点入口,在驶过景点入口6 km时,原路提速返回,恰好与大客车同时到达景点入口.两车距学校的路程S(单位:km)和行驶时间t(单位:min)之间的函数关系如图所示.
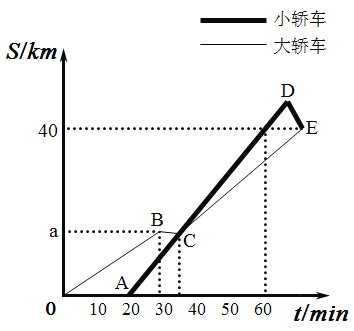
请结合图象解决下面问题:
(1)学校到景点的路程为________km,![]() ________;
________;
(2)在小轿车司机驶过景点入口时,大客车离景点入口还有多远?
(3)小轿车司机到达景点入口时发现本路段限速80 km/h,请你帮助小轿车司机计算折返时是否超速?
【答案】(1)40,15;(2)在小轿车司机驶过景点入口时,大客车离景点入口还有![]() 千米;(3)小轿车折返时已经超速,见解析
千米;(3)小轿车折返时已经超速,见解析
【解析】
(1)根据图象即可知学校到景点的路程,根据速度=路程÷时间可求出小汽车的速度,进而可求出a值;(2)由a的值可求出大客车原来的速度,即可求出提速后的速度,由图象可知小汽车驶过景点入口时的时间,可求出大客车继续行驶的路程,进而可得答案;(3)设直线AF的解析式为![]() ,小汽车驶过景点入口时为点F,根据A、F两点坐标,利用待定系数法可求出直线AF的解析式,根据驶过景点入口6km可求出小汽车到折返点D时的时间,根据大客车的速度可求出大客车继续行驶的时间,即可求出折返的时间,进而可求出折返的速度,与80km/h比较即可得答案.
,小汽车驶过景点入口时为点F,根据A、F两点坐标,利用待定系数法可求出直线AF的解析式,根据驶过景点入口6km可求出小汽车到折返点D时的时间,根据大客车的速度可求出大客车继续行驶的时间,即可求出折返的时间,进而可求出折返的速度,与80km/h比较即可得答案.
(1)由图形可得:学校到景点的路程为40km,
小轿车的速度:![]() (千米/分),
(千米/分),
∵大客车中途停车等候5min,
∴![]() ,
,
故答案为:40,15;
(2)由(1)得:![]() ,得大客车原来的速度:
,得大客车原来的速度:![]() (千米/分),
(千米/分),
小轿车赶上来之后,驶过景点入口时,大客车又行驶了:![]() (千米),
(千米),
∴![]() (千米)
(千米)
答:在小轿车司机驶过景点入口时,大客车离景点入口还有![]() 千米.
千米.
(3)设直线AF的解析式为:![]() ,小汽车驶过景点入口时为点F,
,小汽车驶过景点入口时为点F,
∵![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴直线AF的解析式为:![]()
当![]() 时,
时,![]() ,
,![]() ,小轿车赶上来之后,大客车又行驶的时间:
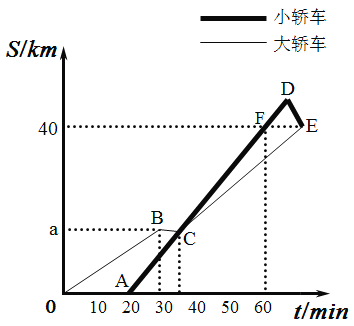
,小轿车赶上来之后,大客车又行驶的时间: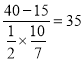 ,
,
小轿车司机折返时的速度:![]() (千米/分)
(千米/分)![]() 千米/时
千米/时![]() 千米/时,
千米/时,
∴小轿车折返时已经超速.


科目:初中数学 来源: 题型:
【题目】如图,A、B两点的坐标分别为(0,6),(0,3),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.

(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(2,0)运动到点(3,0)时,请直接写出线段QM扫过图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
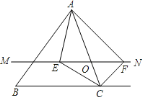
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上(端点除外)的一个动点,过点
边上(端点除外)的一个动点,过点![]() 作直线
作直线![]() .设
.设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,连接
,连接![]() 、
、![]() .那么当点
.那么当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(m+n+1)x+m(n≥0)的两个实数根为α、β,且α≤β.
(1)试用含α、β的代数式表示m和n;
(2)求证:α≤1≤β;
(3)若点P(α,β)在△ABC的三条边上运动,且△ABC顶点的坐标分别为A(1,2)、B(![]() ,1)、C(1,1),问是否存在点P,使m+n=
,1)、C(1,1),问是否存在点P,使m+n=![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形△ABC,BC边上的高恰好等于BC边长的一半,则∠BAC的度数是( )
A.75°B.90°或75°C.90°或 75°或15°D.75°或15°或60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.

②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
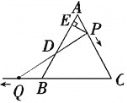
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)若AE=1时,求AP的长;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )

A. 71° B. 76° C. 78° D. 80°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com