
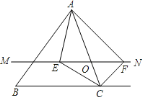
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上(端点除外)的一个动点,过点
边上(端点除外)的一个动点,过点![]() 作直线
作直线![]() .设
.设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,连接
,连接![]() 、
、![]() .那么当点
.那么当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
【答案】当点![]() 运动到
运动到![]() 的中点(或
的中点(或![]() )时,四边形
)时,四边形![]() 是矩形,证明详见解析.
是矩形,证明详见解析.
【解析】
当点O运动到AC的中点(或OA=OC)时,四边形AECF是矩形.由于CE平分∠BCA,那么有∠1=∠2,而MN∥BC,利用平行线的性质有∠1=∠3,等量代换有∠2=∠3,于OE=OC,同理OC=OF,于是OE=OF,而OA=OC,那么可证四边形AECF是平行四边形,又CE、CF分别是∠BCA及其外角的角平分线,易证∠ECF是90°,从而可证四边形AECF是矩形.
当点![]() 运动到
运动到![]() 的中点(或
的中点(或![]() )时,四边形
)时,四边形![]() 是矩形.
是矩形.
证明:∵![]() 平分
平分![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() 是
是![]() 的外角平分线,
的外角平分线,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴平行四边形![]() 是矩形.
是矩形.


科目:初中数学 来源: 题型:
【题目】(1)填写下表,观察被开方数![]() 的小数点与算术平方根
的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
| 0.0016 | 0.16 | 16 | 1600 |
| 0.04 | 0.4 |
(2)根据你发现的规律填空:
①已知![]() ,则
,则![]() .
.
②已知![]() ,
,![]() ,则
,则![]() 是
是![]() 的 倍.
的 倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
关于x的方程:x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() (可变形为x+
(可变形为x+![]() =c+
=c+![]() )的解为x1=c,x2=
)的解为x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Zx+
Zx+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Z.
Z.
(1)归纳结论:根据上述方程与解的特征,得到关于x的方程x+![]() =c+
=c+![]() (m≠0)的解为 .
(m≠0)的解为 .
(2)应用结论:解关于y的方程y﹣a=![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1、x2是一元二次方程2x2﹣7x+5=0的两根,利用一元二次方程根与系数的关系,求下列各式的值.
(1)x12x2+x1x22; (2)(x1﹣x2)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级同学从学校出发去太阳岛研学旅行,一部分乘坐大客车先出发,余下的同学20min后乘坐小轿车沿同一路线出行,大客车中途停车等候5min,小轿车赶上来之后,大客车以出发时速度的![]() 继续行驶,小轿车保持原速度不变.小轿车司机因路线不熟错过了景点入口,在驶过景点入口6 km时,原路提速返回,恰好与大客车同时到达景点入口.两车距学校的路程S(单位:km)和行驶时间t(单位:min)之间的函数关系如图所示.
继续行驶,小轿车保持原速度不变.小轿车司机因路线不熟错过了景点入口,在驶过景点入口6 km时,原路提速返回,恰好与大客车同时到达景点入口.两车距学校的路程S(单位:km)和行驶时间t(单位:min)之间的函数关系如图所示.
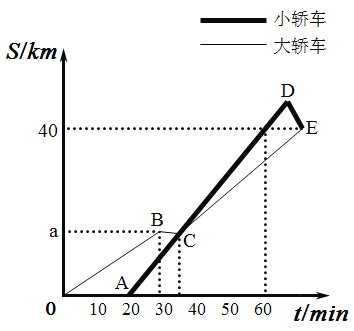
请结合图象解决下面问题:
(1)学校到景点的路程为________km,![]() ________;
________;
(2)在小轿车司机驶过景点入口时,大客车离景点入口还有多远?
(3)小轿车司机到达景点入口时发现本路段限速80 km/h,请你帮助小轿车司机计算折返时是否超速?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击运动员练习射击,![]() 次成绩分别是:
次成绩分别是:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (单位:环).下列说法中正确的是( )
(单位:环).下列说法中正确的是( )
A. 若这![]() 次成绩的中位数为
次成绩的中位数为![]() ,则
,则![]() B. 若这
B. 若这![]() 次成绩的众数是
次成绩的众数是![]() ,则
,则![]()
C. 若这![]() 次成绩的方差为
次成绩的方差为![]() ,则
,则![]() D. 若这
D. 若这![]() 次成绩的平均成绩是
次成绩的平均成绩是![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com