
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.

科目:初中数学 来源: 题型:
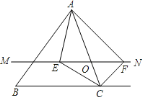
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上(端点除外)的一个动点,过点
边上(端点除外)的一个动点,过点![]() 作直线
作直线![]() .设
.设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,连接
,连接![]() 、
、![]() .那么当点
.那么当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
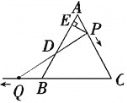
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)若AE=1时,求AP的长;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.

(1)问题:方程x3+x2﹣2x=0的解是x1=0,x2=________,x3=________;
(2)拓展:用“转化”思想求方程![]() =x的解;
=x的解;
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,![]() 点的纵坐标为
点的纵坐标为![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.

![]() 求反比例函数的解析式;
求反比例函数的解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 若点
若点![]() 是反比例函数
是反比例函数![]() 图象上的一点,且满足
图象上的一点,且满足![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,请直接写出点
倍,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )

A. 71° B. 76° C. 78° D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度都为1cm/s.当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t(s).

(1)当t为何值时,△PBQ是直角三角形?
(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC和△AEF中,点E在BC边上,AE=AB,AC=AF,∠CAF=∠BAE,EF与AC交于点G.

(1)求证:EF=BC;
(2)若∠ABC=65°.∠ACB=28°,求∠FGC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com