
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆. 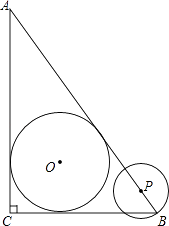
(1)求⊙O的半径;
(2)点P从点B沿边BA向点A以1cm/s的速度匀速运动,以P为圆心,PB长为半径作圆,设点P运动的时间为t s,若⊙P与⊙O相切,求t的值.
【答案】
(1)解:如图1,设⊙O与AB、BC、CA的切点分别为D、E、F,连接OD、OE、OF,
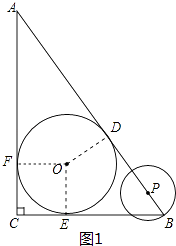
则AD=AF,BD=BE,CE=CF.
∵⊙O为△ABC的内切圆,
∴OF⊥AC,OE⊥BC,即∠OFC=∠OEC=90°.
∵∠C=90°,
∴四边形CEOF是矩形,
∵OE=OF,
∴四边形CEOF是正方形.
设⊙O的半径为rcm,则FC=EC=OE=rcm,
在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,
∴AB= ![]() =5cm.
=5cm.
∵AD=AF=AC﹣FC=4﹣r,BD=BE=BC﹣EC=3﹣r,
∴4﹣r+3﹣r=5,
解得 r=1,即⊙O的半径为1cm.
(2)解:如图2,过点P作PG⊥BC,垂足为G.
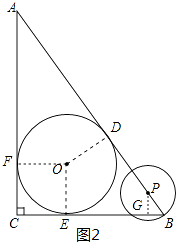
∵∠PGB=∠C=90°,
∴PG∥AC.
∴△PBG∽△ABC,
∴ ![]() .
.
∵BP=t,
∴PG= ![]() =
= ![]() ,BG=
,BG= ![]() =
= ![]() .
.
若⊙P与⊙O相切,则可分为两种情况,⊙P与⊙O外切,⊙P与⊙O内切.
①当⊙P与⊙O外切时,
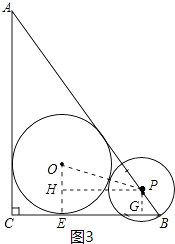
如图3,连接OP,则OP=1+t,过点P作PH⊥OE,垂足为H.
∵∠PHE=∠HEG=∠PGE=90°,
∴四边形PHEG是矩形,
∴HE=PG,PH=GE,
∴OH=OE﹣HE=1﹣ ![]() ,PH=GE=BC﹣EC﹣BG=3﹣1﹣
,PH=GE=BC﹣EC﹣BG=3﹣1﹣ ![]() =2﹣
=2﹣ ![]() .
.
在Rt△OPH中,
由勾股定理, ![]() ,
,
解得 t= ![]() .
.
②当⊙P与⊙O内切时,
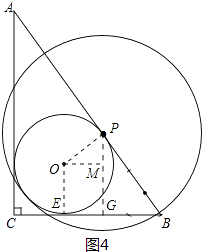
如图4,连接OP,则OP=t﹣1,过点O作OM⊥PG,垂足为M.
∵∠MGE=∠OEG=∠OMG=90°,
∴四边形OEGM是矩形,
∴MG=OE,OM=EG,
∴PM=PG﹣MG= ![]() ,
,
OM=EG=BC﹣EC﹣BG=3﹣1﹣ ![]() =2﹣
=2﹣ ![]() ,
,
在Rt△OPM中,
由勾股定理, ![]() ,
,
解得 t=2.
综上所述,⊙P与⊙O相切时,t= ![]() s或t=2s.
s或t=2s.
另解:外切时,OP2=OD2+DP2.内切时,(t﹣1)2=12的平方加(t﹣2)2.
【解析】(1)求圆的半径,因为相切,我们通常连接切点和圆心,设出半径,再利用圆的性质和直角三角形性质表示其中关系,得到方程,求解即得半径.(2)考虑两圆相切,且一圆已固定,一般就有两种情形,外切与内切.所以我们要分别讨论,当外切时,圆心距等于两圆半径的和;当内切时,圆心距等于大圆与小圆半径的差.分别作垂线构造直角三角形,类似(1)通过表示边长之间的关系列方程,易得t的值.


科目:初中数学 来源: 题型:
【题目】如图,一个半径为r的圆形纸片在边长为a( ![]() )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( ) 
A.![]()
B.![]()
C.![]()
D.πr2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示. 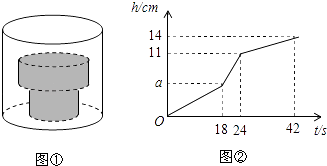
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为cm,匀速注水的水流速度为cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2 , 求“几何体”上方圆柱的高和底面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】具备下列条件的三角形中,不是直角三角形的是( )
A. ∠A+∠B=∠C B. ∠B=∠C=![]() ∠A
∠A
C. ∠A=90°-∠B D. ∠A-∠B=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在以AB为直径的半圆内,连接AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法一定正确的是( ) ①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.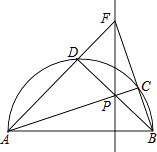
A.①③
B.①④
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.
(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
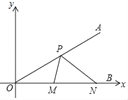
【题目】如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(6,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com