
【题目】解方程
(1)3x2﹣6x+1=0(用配方法)
(2)3(x﹣1)2=x(x﹣1)
【答案】
(1)解:3x2﹣6x+1=0,
3x2﹣6x=﹣1,
x2﹣2x=﹣ ![]() ,
,
x2﹣2x+1=﹣ ![]() +1,
+1,
(x﹣1)2= ![]() ,
,
x﹣1= ![]() ,
,
x1=1+ ![]() ,x2=1﹣
,x2=1﹣ ![]()
(2)解:3(x﹣1)2=x(x﹣1),
3(x﹣1)2﹣x(x﹣1)=0,
(x﹣1)[3(x﹣1)﹣x]=0,
x﹣1=0,3(x﹣1)﹣x=0,
x1=1,x2= ![]()
【解析】(1)移项,系数化成1,配方,开方,即可得出两个一元一次方程,求出方程的解即可;(2)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.
【考点精析】本题主要考查了配方法和因式分解法的相关知识点,需要掌握左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣2x2﹣1向上平移若干个单位,使抛物线与坐标轴有三个交点,如果这些交点能构成直角三角形,那么平移的距离为( )
A.![]() 个单位
个单位
B.1个单位
C.![]() 个单位
个单位
D.![]() 个单位
个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知非直角三角形ABC中,∠A=45°,高BD与CE所在直线交于点H,则∠BHC的度数是( )
A. 45° B. 45° 或125° C. 45°或135° D. 135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ. 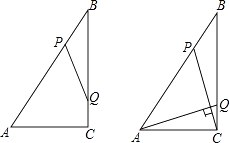
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ,CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣6x﹣16=0
(2)(x﹣3)2=3x(x﹣3)
(3)(x+3)(x﹣2)=50
(4)(2x+1)2+3(2x+1)+2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②﹣b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( ) 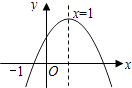
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,⊙O为△ABC的内切圆. 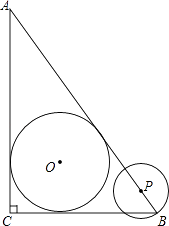
(1)求⊙O的半径;
(2)点P从点B沿边BA向点A以1cm/s的速度匀速运动,以P为圆心,PB长为半径作圆,设点P运动的时间为t s,若⊙P与⊙O相切,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com