
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②﹣b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( ) 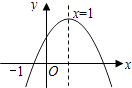
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=﹣ ![]() ,
,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
根据图象知道当x=﹣1时,y=a﹣b+c<0,
∴a+c<b,故②错误;
根据图象知道当x=2时,y=4a+2b+c>0,故③正确;
根据图象知道抛物线与x轴有两个交点,
∴b2﹣4ac>0,故④正确.
正确的有③④.
故选:B.
首先根据开口方向确定a的取值范围,根据对称轴的位置确定b的取值范围,根据抛物线与y轴的交点确定c的取值范围,根据抛物线与x轴是否有交点确定b2﹣4ac的取值范围,根据图象和x=2的函数值即可确定4a+2b+c的取值范围,根据x=1的函数值可以确定b<a+c是否成立.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,把抛物线y= ![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= ![]() x2交于点Q,则图中阴影部分的面积为 .
x2交于点Q,则图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
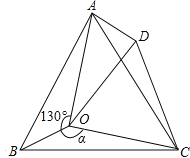
【题目】如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)判断△COD的形状,并加以说明理由.
(2)若AD=1,OC=![]() ,OA=
,OA=![]() 时,求α的度数.
时,求α的度数.
(3)探究:当α为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=y1﹣y2 , y1与x2成正比例,y2与x﹣1成反比例,当x=﹣1时,y=3;当x=2时,y=﹣3.
(1)求y与x之间的函数关系;
(2)当x= ![]() 时,求y的值.
时,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为r的圆形纸片在边长为a( ![]() )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( ) 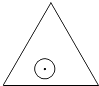
A.![]()
B.![]()
C.![]()
D.πr2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示. 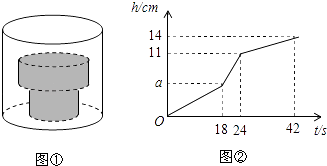
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为cm,匀速注水的水流速度为cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2 , 求“几何体”上方圆柱的高和底面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.
(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com