
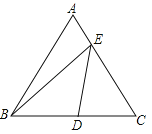
【题目】(2015攀枝花,第15题,4分)如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为_____.
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ. 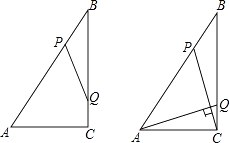
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ,CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣6x﹣16=0
(2)(x﹣3)2=3x(x﹣3)
(3)(x+3)(x﹣2)=50
(4)(2x+1)2+3(2x+1)+2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②﹣b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( ) 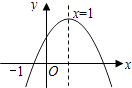
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师在课堂上提出一个问题:“通过探究知道: ![]() ≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用
≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用![]() ﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:
(1)![]() 的小数部分是a,
的小数部分是a, ![]() 的整数部分是b,求a+b﹣
的整数部分是b,求a+b﹣![]() 的值.
的值.
(2)已知8+![]() =x+y,其中x是一个整数,0<y<1,求3x+(y﹣
=x+y,其中x是一个整数,0<y<1,求3x+(y﹣![]() )2018的值.
)2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据以下10个乘积,回答问题:
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)试将以上各乘积分别写成一个平方差的形式,并写出其中一个的思考过程
(2)将以上10个乘积按照从小到大排列起来
(3)若用![]() ,
,![]() ,
,![]() ,....
,....![]() ,表示n个乘积,其中
,表示n个乘积,其中![]() 为正数,试由(1)(2)猜测一个一般性的结论。(不要求写证明)
为正数,试由(1)(2)猜测一个一般性的结论。(不要求写证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com