
【题目】解方程:
(1)x2﹣6x﹣16=0
(2)(x﹣3)2=3x(x﹣3)
(3)(x+3)(x﹣2)=50
(4)(2x+1)2+3(2x+1)+2=0.
【答案】
(1)解:原方程变形为(x﹣8)(x+2)=0
x﹣8=0或x+2=0
∴x1=8,x2=﹣2
(2)解:(x﹣3)2=3x(x﹣3),
(x﹣3)(1﹣3x)=0,
则x﹣3=0或1﹣3x=0,
∴x1=3,x2= ![]()
(3)解:(x+3)(x﹣2)=50,
x2+x﹣56=0,
(x﹣7)(x+8)=0,
则x﹣7=0或x+8=0,
∴x1=7,x2=﹣8.
(4)解:设2x+1=t,则
t2+3t+2=0,
(t+1)2+(t+2)=0.
t=﹣1或t=﹣2,
故2x+1=﹣1或2x+1=﹣2,
∴x1=﹣1,x2=﹣1.5
【解析】(1)解此一元二次方程选择因式分解法最简单,因为﹣16=﹣8×2,﹣6=﹣8+2,所以x2﹣6x﹣16=(x﹣8)(x+2),这样即达到了降次的目的.(2)先移项,然后利用提取公因式对等式的左边进行因式分解,再来解方程即可;(3)先把原方程转化为一般式方程,然后利用因式分解法解方程;(4)利用换元法解方程.
【考点精析】解答此题的关键在于理解因式分解法的相关知识,掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势.


科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面. 
(1)请找出截面的圆心;(不写画法,保留作图痕迹.)
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)![]() +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;
(2)如果(2+![]() )a-(1-
)a-(1-![]() )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,点D的坐标是(0, ![]() ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.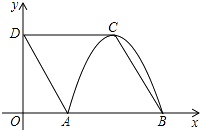
(1)求A,B,C三点的坐标;
(2)求过A,B,C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
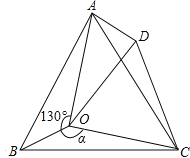
【题目】如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)判断△COD的形状,并加以说明理由.
(2)若AD=1,OC=![]() ,OA=
,OA=![]() 时,求α的度数.
时,求α的度数.
(3)探究:当α为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为r的圆形纸片在边长为a( ![]() )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( ) 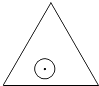
A.![]()
B.![]()
C.![]()
D.πr2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在以AB为直径的半圆内,连接AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法一定正确的是( ) ①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.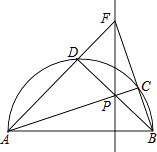
A.①③
B.①④
C.②④
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com