练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一个半径为r的圆形纸片在边长为a（ ）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）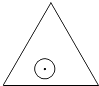
    A.
    B.
    C.
    D.πr2

    【答案】C
    【解析】解：如图，当圆形纸片运动到与∠A的两边相切的位置时， 过圆形纸片的圆心O1作两边的垂线，垂足分别为D，E，
    连AO1 ， 则Rt△ADO1中，∠O1AD=30°，O1D=r， ．
    ∴ ．由 ．
    ∵由题意，∠DO1E=120°，得 ，
    ∴圆形纸片不能接触到的部分的面积为 = ．
    故选：C．

    过圆形纸片的圆心O1作两边的垂线，垂足分别为D，E，连AO1 ， 则在Rt△ADO1中，可求得 ．四边形ADO1E的面积等于三角形ADO1的面积的2倍，还可求出扇形O1DE的面积，所求面积等于四边形ADO1E的面积减去扇形O1DE的面积的三倍．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知非直角三角形ABC中，∠A=45°，高BD与CE所在直线交于点H，则∠BHC的度数是（ ）

    A. 45° B. 45° 或125° C. 45°或135° D. 135°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：
    （1）x2﹣6x﹣16=0
    （2）（x﹣3）2=3x（x﹣3）
    （3）（x+3）（x﹣2）=50
    （4）（2x+1）2+3（2x+1）+2=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc＞0；②﹣b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0；其中正确的结论有（ ）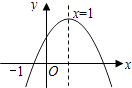

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB边的垂直平分线交BC于D，AC边的垂直平分线交BC于E， 与相交于点O，△ADE的周长为6cm．

    （1）求BC的长；

    （2）分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学老师在课堂上提出一个问题：“通过探究知道： ≈1.414…，它是个无限不循环小数，也叫无理数，它的整数部分是1，那么有谁能说出它的小数部分是多少”，小明举手回答：它的小数部分我们无法全部写出来，但可以用﹣1来表示它的小数部分，张老师夸奖小明真聪明，肯定了他的说法．现请你根据小明的说法解答：

    （1）的小数部分是a， 的整数部分是b，求a+b﹣的值．

    （2）已知8+=x+y，其中x是一个整数，0＜y＜1，求3x+（y﹣）2018的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在四边形ABCD中，∠A=90°，AD=6，AB=8,BC=26,CD=24

    （1）求四边形ABCD的面积．

    （2）求D到BC的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=4cm，BC=3cm，⊙O为△ABC的内切圆．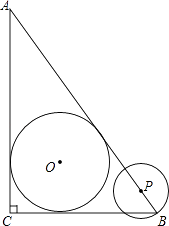
    （1）求⊙O的半径；
    （2）点P从点B沿边BA向点A以1cm/s的速度匀速运动，以P为圆心，PB长为半径作圆，设点P运动的时间为t s，若⊙P与⊙O相切，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，矩形OABC顶点B的坐标为（8，3），定点D的坐标为（12，0），动点P从点O出发，以每秒2个单位长度的速度沿x轴的正方向匀速运动，动点Q从点D出发，以每秒1个单位长度的速度沿x轴的负方向匀速运动，PQ两点同时运动，相遇时停止．在运动过程中，以PQ为斜边在x轴上方作等腰直角三角形PQR．设运动时间为t秒．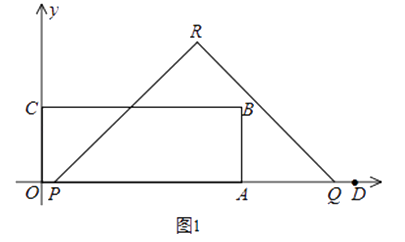

    （1）当t=时，△PQR的边QR经过点B；
    （2）设△PQR和矩形OABC重叠部分的面积为S，求S关于t的函数关系式；
    （3）如图2，过定点E（5，0）作EF⊥BC，垂足为F，当△PQR的顶点R落在矩形OABC的内部时，过点R作x轴、y轴的平行线，分别交EF、BC于点M、N，若∠MAN=45°，求t的值．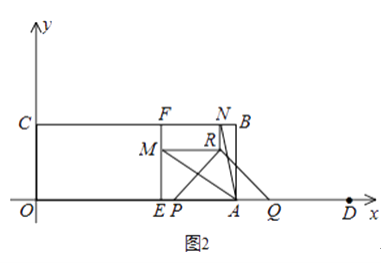

    查看答案和解析>>

    同步练习册答案