
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面. 
(1)请找出截面的圆心;(不写画法,保留作图痕迹.)
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
【答案】
(1)解:如图所示
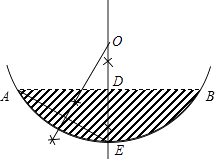
(2)解:如图,OE⊥AB交AB于点D,
则DE=4cm,AB=16cm,AD=8cm,
设半径为Rcm,则
OD=OE﹣DE=R﹣4,
由勾股定理得,OA2=AD2+OD2,
即R2=82+(R﹣4)2,
解得R=10.
故这个圆形截面的半径是10cm

【解析】(1)根据尺规作图的步骤和方法做出图即可;(2)先作辅助线,利用垂径定理求出半径,再根据勾股定理计算.
【考点精析】关于本题考查的垂径定理的推论,需要了解推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等才能得出正确答案.


科目:初中数学 来源: 题型:
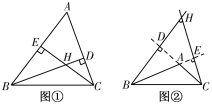
【题目】(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H.找出∠BHC和∠A之间存在何种等量关系;
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,把图②补充完整,并指出此时(1)中的等量关系是否仍然成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣2x2﹣1向上平移若干个单位,使抛物线与坐标轴有三个交点,如果这些交点能构成直角三角形,那么平移的距离为( )
A.![]() 个单位
个单位
B.1个单位
C.![]() 个单位
个单位
D.![]() 个单位
个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数. 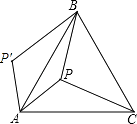
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系种中,点![]()
![]() 点
点![]() 关于
关于![]() 轴对称的点的坐标是:________;
轴对称的点的坐标是:________;
![]() 点
点![]() 关于
关于![]() 轴对称的点的坐标是:________;
轴对称的点的坐标是:________;
![]() 点
点![]() 关于原点对称的点的坐标是:________;
关于原点对称的点的坐标是:________;
![]() 将点
将点![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后,得到的点的坐标是:________;
后,得到的点的坐标是:________;
![]() 将点
将点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() 后,得到的点的坐标是:________;
后,得到的点的坐标是:________;
![]() 将点
将点![]() 绕另一点
绕另一点![]() 旋转
旋转![]() 得到点
得到点![]() ,则
,则![]() 点的坐标为________.
点的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知非直角三角形ABC中,∠A=45°,高BD与CE所在直线交于点H,则∠BHC的度数是( )
A. 45° B. 45° 或125° C. 45°或135° D. 135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣6x﹣16=0
(2)(x﹣3)2=3x(x﹣3)
(3)(x+3)(x﹣2)=50
(4)(2x+1)2+3(2x+1)+2=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com