
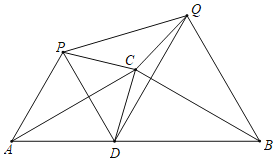
【题目】如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ.
(1)证明:CP=CQ;
(2)求∠PCQ的度数;
(3)当点D是AB中点时,请直接写出△PDQ是何种三角形.
【答案】(1)见解析;(2)∠PCQ=120°;(3)△PDQ是等边三角形.
【解析】
(1)由折叠直接得到结论;
(2)由折叠的性质求出∠ACP+∠BCQ=120°,再用周角的意义求出∠PCQ=120°;
(3)先判断出△APD是等边三角形,△BDQ是等边三角形,再求出∠PDQ=60°,即可.
(1)∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴CP=CD=CQ;
(2)∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴∠ACP=∠ACD,∠BCQ=∠BCD,
∴∠ACP+∠BCQ=∠ACD+∠BCD=∠ACB=120°,
∴∠PCQ=360°-(∠ACP+BCQ+∠ACB)=360°-(120°+120°)=120°;
(3)△PDQ是等边三角形.
理由:∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴AD=AP,∠DAC=∠PAC,
∵∠DAC=30°,
∴∠PAD=60°,
∴△APD是等边三角形,
∴PD=AD,∠ADP=60°,
同理:△BDQ是等边三角形,
∴DQ=BD,∠BDQ=60°,
∴∠PDQ=60°,
∵当点D在AB的中点,
∴AD=BD,
∴PD=DQ,
∴△DPQ是等边三角形


科目:初中数学 来源: 题型:
【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.
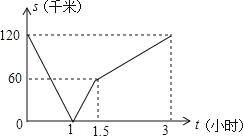
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.

(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的![]() ;
;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸上的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣2,﹣1).
(1)把△ABC向左平移4格后得到△A1B1C1,画出△A1B 1C1并写出点A1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
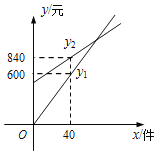
【题目】某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少8元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用):
(1)求y1的函数解析式;
(2)请问方案二中每月付给销售人员的底薪是多少元?
(3)小丽应选择哪种销售方案,才能使月工资更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),C(0,3)
(1)求该抛物线的表达式;
(2)求BC的解析式;
(3)点M是对称轴右侧点B左侧的抛物线上一个动点,当点M运动到什么位置时,△BCM的面积最大?求△BCM面积的最大值及此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点![]() 是线段
是线段![]() 外,且
外,且![]() ,求证:点
,求证:点![]() 在线段
在线段![]() 的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
A. 作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() B. 过点
B. 过点![]() 作
作![]() 于点
于点![]() 且
且![]()
C. 取![]() 中点
中点![]() ,连接
,连接![]() D. 过点
D. 过点![]() 作
作![]() ,垂足为
,垂足为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
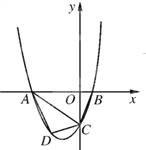
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A, B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,过点D做x轴的垂线,交AC于点E,求线段DE的最大值.
(3)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com