
【题目】已知:如图,点![]() 是线段
是线段![]() 外,且
外,且![]() ,求证:点
,求证:点![]() 在线段
在线段![]() 的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
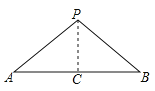
A. 作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() B. 过点
B. 过点![]() 作
作![]() 于点
于点![]() 且
且![]()
C. 取![]() 中点
中点![]() ,连接
,连接![]() D. 过点
D. 过点![]() 作
作![]() ,垂足为
,垂足为![]()
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
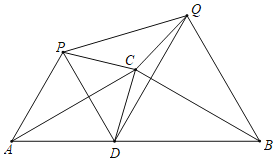
【题目】如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ.
(1)证明:CP=CQ;
(2)求∠PCQ的度数;
(3)当点D是AB中点时,请直接写出△PDQ是何种三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,若 P是口ABCD 边 CD 上任意一点,连结 AP、BP,若△APB 的面积为 60 ,△APD 的面积为 18,则 S△APC= .
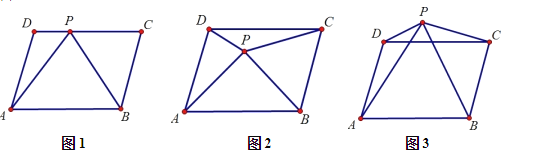
(2) 如图 2,①若点 P 运动到口ABCD 内一点时,试说明 S△APB +S△DPC =S△BPC +S△APD.
②若此时△APB 的面积为 60,△APD 的面积为 18,则 S△APC= .
(3)如图 3①利用(2)中的方法你会发现,S△APB ,S△DPC ,S△BPC ,S△APD 之间存在怎样的关系: .
②若此时△APB 的面积为 60,△APD 的面积为 18,请利用你的发现,求 S△APC 的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有足够多除颜色外均相同的球,请你从中选![]() 个球设计摸球游戏.
个球设计摸球游戏.
(1)使摸到红球的概率和摸到白球的概率相等;
(2)使摸到红球、白球、黑球的概率都相等;
(3)使摸到红球的概率和摸到白球的概率相等,且都小于摸到黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用0.8万元购进这种衬衫,面市后果然供不应求.于是,商厦又用1.76万元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了4元,商厦销售这种衬衫时每件预定售价都是58元.
(1)求这种衬衫原进价为每件多少元?
(2)经过一段时间销售,根据市场饱和情况,商厦经理决定对剩余的100件衬衫进行打折销售,以提高回款速度,要使这两批衬衫的总利润不少于6300元,最多可以打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
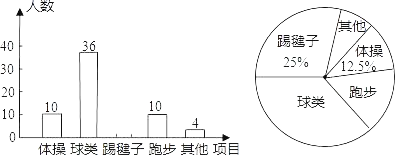
【题目】为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图(均不完整).
(1)补全频数分布直方图;
(2)求扇形统计图中表示“踢毽子”项目扇形圆心角的度数.
(3)估计该校1800名学生中有多少人最喜爱球类活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留一丝空隙,又不互相重叠(在数学上叫做平面镶嵌).这显然与正多边形的内角大小有关,当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请你根据图中的图形,填写表中空格:

正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
正多边形每个内角度数 | 60° | 90° | 108° | 120° | …… |
(2)如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com