
【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留一丝空隙,又不互相重叠(在数学上叫做平面镶嵌).这显然与正多边形的内角大小有关,当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请你根据图中的图形,填写表中空格:

正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
正多边形每个内角度数 | 60° | 90° | 108° | 120° | …… |
(2)如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,点![]() 是线段
是线段![]() 外,且
外,且![]() ,求证:点
,求证:点![]() 在线段
在线段![]() 的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
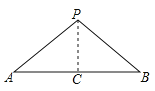
A. 作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() B. 过点
B. 过点![]() 作
作![]() 于点
于点![]() 且
且![]()
C. 取![]() 中点
中点![]() ,连接
,连接![]() D. 过点
D. 过点![]() 作
作![]() ,垂足为
,垂足为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
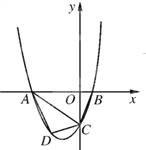
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A, B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,过点D做x轴的垂线,交AC于点E,求线段DE的最大值.
(3)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气频发,市场上防护口罩出现热销.某药店准备购进一批![]() 两种不同型号口罩进行销售.下表是甲、乙两人购买
两种不同型号口罩进行销售.下表是甲、乙两人购买![]() 两种型号口罩的情况:
两种型号口罩的情况:
A型号数量(单位:个) | B型号数量(单位:个) | 总售价(单位:元) | |
甲 | 1 | 3 | 26 |
乙 | 3 | 2 | 29 |
(1)求一个![]() 型口罩和一个
型口罩和一个![]() 型口罩的售价各是多少元?
型口罩的售价各是多少元?
(2)药店准备购进这两种型号的口罩共50个,其中![]() 型口罩数量不少于35个,且不多于
型口罩数量不少于35个,且不多于![]() 型口罩的3倍,有几种购买方案?请写出购买方案.
型口罩的3倍,有几种购买方案?请写出购买方案.
(3)在(2)的条件下,药店在销售完这批口罩后,总售价能否达到282元?
查看答案和解析>>
科目:初中数学 来源: 题型:
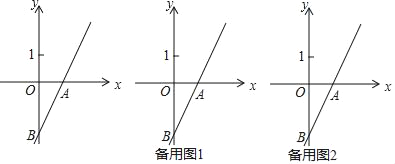
【题目】如图,直线y=2x﹣2与x轴交于点A,与y轴交于点B.点C是该直线上不同于B的点,且CA=AB.
(1)写出A、B两点坐标;
(2)过动点P(m,0)且垂直于x轴的直线与直线AB交于点D,若点D不在线段BC上,求m的取值范围;
(3)若直线BE与直线AB所夹锐角为45°,请直接写出直线BE的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负贵了解他所居住的小区450户居民的家庭收入情况从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频分布直方图。

分组 | 频数 | 百分比 |
600≤ | 2 | 5% |
800≤ | 6 | 15% |
1000≤ | 45% | |
9 | 22.5% | |
1400≤ | ||
1600≤ | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题
(1)补全频数分布表
(2)补全频数分布直方图
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4![]() ,
, ![]()
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(2,-3)、P(3,![]() )、Q(-5,b)都在反比例函数的图象y=
)、Q(-5,b)都在反比例函数的图象y=![]() (k≠0)上.
(k≠0)上.
(1)求此反比例函数解析式;
(2)求a+![]() 的值;
的值;
(3)若反比例函数y=![]() 经过A′(2,3),点P和点Q关于y轴的对称点P′、Q′在反比例函数y=
经过A′(2,3),点P和点Q关于y轴的对称点P′、Q′在反比例函数y=![]() 的图象上吗?通过计算说明理由.
的图象上吗?通过计算说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com