
【题目】如图,直线y=2x﹣2与x轴交于点A,与y轴交于点B.点C是该直线上不同于B的点,且CA=AB.
(1)写出A、B两点坐标;
(2)过动点P(m,0)且垂直于x轴的直线与直线AB交于点D,若点D不在线段BC上,求m的取值范围;
(3)若直线BE与直线AB所夹锐角为45°,请直接写出直线BE的函数解析式.
【答案】(1)A(1,0),B(0,﹣2);(2)m<0或m>2;(3)y=![]() x﹣2或y=﹣3x﹣2.
x﹣2或y=﹣3x﹣2.
【解析】
(1)利用待定系数法即可解决问题;
(2)如图1中,作CF⊥x轴与F.利用全等三角形的性质求出点F坐标即可判断;
(3)如图2中,作AE⊥AB,使得AE=AB,作EH⊥x轴于H,则△ABE是等腰直角三角形,∠ABE=45°.利用全等三角形的性质求出点E坐标,当直线BE′⊥直线BE时,直线BE′也满足条件,求出直线BE′的解析式即可;
解:(1)对于直线y=2x﹣2令x=0,得到y=﹣2,令y=0,得到x=1,
∴A(1,0),B(0,﹣2).
(2)如图1中,作CF⊥x轴与F.
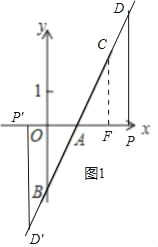
∵CA=AB,∠CAF=∠OAB,∠CFA=∠AOB=90°,
∴△CAF≌△BAO,
∴AF=OA=1,CF=OB=2,
∴F(2,0),
观察图象可知m的取值范围为:m<0或m>2.
(3)如图2中,作AE⊥AB,使得AE=AB,作EH⊥x轴于H,则△ABE是等腰直角三角形,∠ABE=45°.
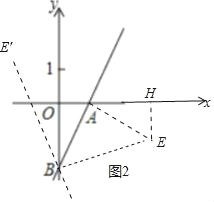
∵∠AOB=∠BAE=∠AHE=90°,
∴∠OAB+∠ABO=90°,∠OAB+∠HAE=90°,
∴∠ABO=∠HAE,∵AB=AE,
∴△ABO≌△EAH,
∴AH=OB=2,EH=OA=1,
∴E(3,﹣1),
设直线BE的解析式为y=kx+b,则有![]()
解得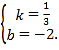
∴直线BE的解析式为![]() ,
,
当直线BE′⊥直线BE时,直线BE′也满足条件,直线BE′的解析式为y=﹣3x﹣2,
∴满足条件的直线BE的解析式为![]() 或y=﹣3x﹣2.
或y=﹣3x﹣2.


科目:初中数学 来源: 题型:
【题目】现有足够多除颜色外均相同的球,请你从中选![]() 个球设计摸球游戏.
个球设计摸球游戏.
(1)使摸到红球的概率和摸到白球的概率相等;
(2)使摸到红球、白球、黑球的概率都相等;
(3)使摸到红球的概率和摸到白球的概率相等,且都小于摸到黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtABC 中, BAC 90, AB AC ,点 D 是 AB 的中点,AF CD 于 H 交 BC 于 F, BE AC 交 AF 的延长线于 E.
求证:(1)ADC ≌ BEA
(2)BC 垂直平分 DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个进行数值转换的运行程序如图所示,从“输入有理数![]() ”到“结果是否大于0”称为“一次操作”
”到“结果是否大于0”称为“一次操作”

(1)下面命题是真命题有( )
①当输入![]() 后,程序操作仅进行一次就停止.
后,程序操作仅进行一次就停止.
②当输入![]() 后,程序操作仅进行一次就停止
后,程序操作仅进行一次就停止
③当输入![]() 为负数时,无论x取何负数,输出的结果总比输入数大.
为负数时,无论x取何负数,输出的结果总比输入数大.
④当输入![]() ,程序操作仅进行一次就停止
,程序操作仅进行一次就停止
A.4 B.3 C.2 D.1
(2)探究:是否存在正整数![]() ,使程序只能进行两次操作,并且输出结果小于12?若存在,请求出所有符合条件的
,使程序只能进行两次操作,并且输出结果小于12?若存在,请求出所有符合条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留一丝空隙,又不互相重叠(在数学上叫做平面镶嵌).这显然与正多边形的内角大小有关,当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请你根据图中的图形,填写表中空格:

正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
正多边形每个内角度数 | 60° | 90° | 108° | 120° | …… |
(2)如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2﹣(2m+1)x+2m=0
(1)求证:方程一定有两个实数根;
(2)若方程的两根为x1,x2,且|x1|=|x2|,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
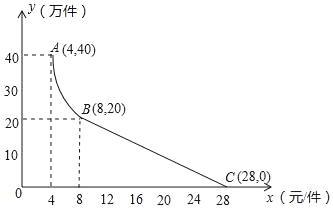
【题目】月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值.
(3)假设公司的这种电子产品第一年恰好按年利润s(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格x(元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润s(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB:y=﹣x+b分别与x,y轴交于A(6,0)、B 两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
(1)求点B的坐标.
(2)求直线BC的解析式.
(3)直线 EF 的解析式为y=x,直线EF交AB于点E,交BC于点 F,求证:S△EBO=S△FBO.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com