
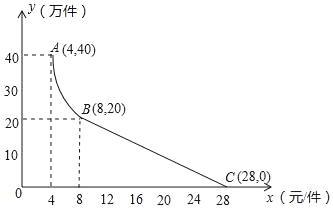
����Ŀ���µ�Ƽ�����˾��160��Ԫ����Ϊ�²�Ʒ���з����ã��ɹ����Ƴ���һ���г�����ĵ��Ӳ�Ʒ�����ڵ���Ͷ���������������ۣ���֪�������ֵ��Ӳ�Ʒ�ijɱ�Ϊ4Ԫ/���������۹����з��֣�ÿ�����������y������������ۼ۸�x��Ԫ/�����Ĺ�ϵ��ͼ��ʾ������ABΪ����������ͼ���һ���֣�BCΪһ�κ���ͼ���һ���֣��蹫˾�������ֵ��Ӳ�Ʒ��������Ϊs����Ԫ������ע������һ��ӯ������ӯ����������һ�������������һ���������������һ��ijɱ�����
��1�������y���������x��Ԫ/����֮��ĺ�����ϵʽ��
��2�������һ�����ֵ��Ӳ�Ʒ��������s����Ԫ����x��Ԫ/����֮��ĺ�����ϵʽ���������һ������������ֵ��
��3�����蹫˾�����ֵ��Ӳ�Ʒ��һ��ǡ�ð�������s����Ԫ��ȡ�����ֵʱ�������ۣ��ָ��ݵ�һ���ӯ������������ڶ��꽫���ֵ��Ӳ�Ʒÿ�������ۼ۸�x��Ԫ������8Ԫ���ϣ�x��8�������ڶ������������103��Ԫʱ������������s����Ԫ�������ۼ۸�x��Ԫ/�����ĺ���ʾ��ͼ�������ۼ۸�x��Ԫ/������ȡֵ��Χ��
���𰸡���1��y=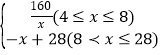 ����2����ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ��16��Ԫ����3��ͼ����������11��x��21ʱ���ڶ����������s������103��Ԫ��
����2����ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ��16��Ԫ����3��ͼ����������11��x��21ʱ���ڶ����������s������103��Ԫ��
�������������������1�����ݴ���ϵ�������������y���������x��Ԫ/����֮��ĺ�����ϵʽ��
��2������������������ۣ���x=8ʱ��zmax=-80����x=16ʱ��zmax=-16������-16>-80���ɵõ�ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ-16��Ԫ��
��3�����ݵڶ����������z=��x-4����-x+28��-16=-x2+32x-128����z=103���ɵ÷���103=-x2+32x-128�����x1=11��x2=21��Ȼ����ƽ��ֱ������ϵ�У�����z��x�ĺ���ͼ����ͼ�ɵó����ۼ۸�x��Ԫ/������ȡֵ��Χ��
�����������1����4��x��8ʱ����y=![]() ����A��4��40�������k=4��40=160��
����A��4��40�������k=4��40=160��
��y��x֮��ĺ�����ϵʽΪy=![]() ��
��
��8��x��28ʱ����y=k'x+b����B��8��20����C��28��0������,
��: ![]() �����
�����![]() ��
��
��y��x֮��ĺ�����ϵʽΪy=��x+28��
����������y= ��
��
��2����4��x��8ʱ��s=��x��4��y��160=��x��4��![]() ��160=��
��160=��![]() ��
��
�ߵ�4��x��8ʱ��s����x�����������
�൱x=8ʱ��smax=��![]() =��80��
=��80��
��8��x��28ʱ��s=��x��4��y��160=��x��4������x+28����160=����x��16��2��16��
�൱x=16ʱ��smax=��16��
����16����80��
�൱ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ��16��Ԫ��
��3���ߵ�һ���������Ϊ��16��Ԫ��
��16��ԪӦ��Ϊ�ڶ���ijɱ���
�֡�x��8��
��ڶ����������s=��x��4������x+28����16=��x2+32x��128��
��s=103����103=��x2+32x��128��
���x1=11��x2=21��
��ƽ��ֱ������ϵ�У�����s��x�ĺ���ʾ��ͼ�ɵã�
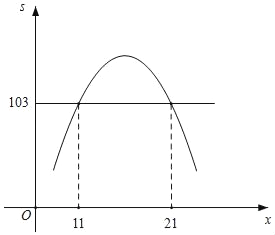
�۲�ʾ��ͼ��֪����s��103ʱ��11��x��21��
�൱11��x��21ʱ���ڶ����������s������103��Ԫ��


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳�����1����λ���ȣ�Rt��ABC����������A(-2��2)��B(0��5)��C(0��2).
(1)����ABC�Ե�CΪ��ת������ת180�����õ���A1B1C���뻭����A1B1C��ͼ��.
(2)ƽ����ABC��ʹ��A�Ķ�Ӧ��A2����Ϊ(-2��-6)���뻭��ƽ�ƺ��Ӧ����A2B2C2��ͼ��.
(3)������A1B1C��ijһ����ת�ɵõ���A2B2C2����ֱ��д����ת���ĵ�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
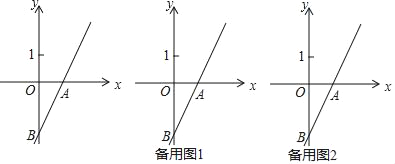
����Ŀ����ͼ��ֱ��y=2x��2��x�ύ�ڵ�A����y�ύ�ڵ�B����C�Ǹ�ֱ���ϲ�ͬ��B�ĵ㣬��CA=AB��
��1��д��A��B�������ꣻ
��2��������P��m��0���Ҵ�ֱ��x���ֱ����ֱ��AB���ڵ�D������D�����߶�BC�ϣ���m��ȡֵ��Χ��
��3����ֱ��BE��ֱ��AB�������Ϊ45�㣬��ֱ��д��ֱ��BE�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��y�Ķ�Ԫһ�η�����![]() �ĽⶼΪ������
�ĽⶼΪ������
(1)��a��ȡֵ��Χ��
(2)����|a+1||a1|��
(3)��������Ԫһ�η�����Ľ���һ�����������ε�һ������һ���ױߵij�����������������ε��ܳ�Ϊ9����a��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���Ѿ���ֽƬOABC����ֱ������ϵxOy�У�ʹOA��OC�ֱ�����x��y����������ϣ�����AC����AC=4![]() ��
�� ![]()
��1����AC����ֱ�ߵĽ���ʽ��
��2����ֽƬOABC�۵���ʹ��A���C�غϣ��ۺ�ΪEF�������۵���ֽƬ�ص����ֵ������
��3����EF���ڵ�ֱ�ߵĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
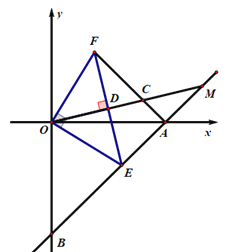
����Ŀ����ͼ��ֱ��AB��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��0����4��������E���߶�AB�ϣ�OE��OF����OE��OF������AF.
��1�������߶�AF��BE֮��Ĺ�ϵ����֤����
��2������O��OM��EF����ΪD,OM�ֱ�AF��BA���ӳ����ڵ�C��M��BE=![]() ����CF�ij�.
����CF�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ؽ�����Ϊ�˷ḻ����ѧ���Ĵ�μ���Ҫ���ѧУ��չ��ʽ�����������������ij��ѧ����ѧ���������Ȥ�����������⣬��������˱�Уij���ѧ���������ݵ��������Ƴ����µIJ�����������ͳ��ͼ������ͳ��ͼ��

��1������ε����У�ϲ��������Ŀ��ͬѧ���� ���ˣ�������ͳ��ͼ�У���ƹ�������İٷֱ�Ϊ�� ��%�����ѧУ��800��ѧ��������ȫУѧ�������� ����ϲ��������Ŀ��
��2���뽫����ͳ��ͼ����������
��3���ڱ������ѧ���У�ϲ���������2��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ2��ͬѧ�����༶�μ�У����ӣ���ֱ��д������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľߵ��е���Ϊ10Ԫ��15Ԫ��20Ԫ�������ľߺг��ۣ����̵�ͳ����2014��3�·��������ľߺе����������������ͳ��ͼ�������������£�

��1����ε�����һ����ȡ�˶��ٸ��ľߺУ�
��2�����ͼ1�б�ʾ��15Ԫ����������ռԲ�ĽǵĶ�����
��3����ͼ2�а�����ͳ��ͼ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͬʱ��ɽ���������˾����ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ����������⣺
��1����ɽ���ٶ����� ����/���ӣ�����A������ʱ�����ĸ߶�bΪ�� ���ף�
��2���������ٺ��ҵ��ٶ��Ǽ�ɽ�ٶȵ�3��������������ٺ�y��x֮��ĺ�����ϵʽ��
��3����ɽ�ʱ��ʱ�������˼ף���ʱ�Ҿ�A�صĸ߶�Ϊ�����ף�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com