
【题目】若关于x、y的二元一次方程组![]() 的解都为正数。
的解都为正数。
(1)求a的取值范围;
(2)化简|a+1||a1|;
(3)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求a的值
【答案】(1)a>1;(2)2;(3)2
【解析】
(1)先解方程组用含a的代数式表示x,y的值,再代入有关x,y的不等关系得到关于a的不等式求解即可;
(2)根据绝对值的定义即可得到结论;
(3)首先用含m的式子表示x和y,由于x、y的值是一个等腰三角形两边的长,所以x、y可能是腰也可能是底,依次分析即可解决,注意应根据三角形三边关系验证是否能组成三角形.
(1)解![]() 得∴
得∴![]() ,
,
∵若关于x、y的二元一次方程组![]() 的解都为正数,
的解都为正数,
∴a>1;
(2)∵a>1,
∴|a+1||a1|=a+1a+1=2;
(3)∵二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,这个等腰三角形的周长为9
∴2(a1)+a+2=9,
解得:a=3,
∴x=2,y=5,不能组成三角形,
∴2(a+2)+a1=9,
解得:a=2,
∴x=1,y=5,能组成等腰三角形,
∴a的值是2.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为直角边且在
为直角边且在![]() 的右侧作等腰直角三角形
的右侧作等腰直角三角形![]() ,
,![]() ,
,![]() .
.

(1)如果![]() ,
,![]() .
.
①当点![]() 在线段
在线段![]() 上时,如图1,线段
上时,如图1,线段![]() 、
、![]() 的位置关系为___________,数量关系为_____________
的位置关系为___________,数量关系为_____________
②当点![]() 在线段
在线段![]() 的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动。探究:当
上运动。探究:当![]() 多少度时,
多少度时,![]() ?小明通过(1)的探究,猜想
?小明通过(1)的探究,猜想![]() 时,
时,![]() .他想过点
.他想过点![]() 做
做![]() 的垂线,与
的垂线,与![]() 的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个进行数值转换的运行程序如图所示,从“输入有理数![]() ”到“结果是否大于0”称为“一次操作”
”到“结果是否大于0”称为“一次操作”

(1)下面命题是真命题有( )
①当输入![]() 后,程序操作仅进行一次就停止.
后,程序操作仅进行一次就停止.
②当输入![]() 后,程序操作仅进行一次就停止
后,程序操作仅进行一次就停止
③当输入![]() 为负数时,无论x取何负数,输出的结果总比输入数大.
为负数时,无论x取何负数,输出的结果总比输入数大.
④当输入![]() ,程序操作仅进行一次就停止
,程序操作仅进行一次就停止
A.4 B.3 C.2 D.1
(2)探究:是否存在正整数![]() ,使程序只能进行两次操作,并且输出结果小于12?若存在,请求出所有符合条件的
,使程序只能进行两次操作,并且输出结果小于12?若存在,请求出所有符合条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程x2﹣(2m+1)x+2m=0
(1)求证:方程一定有两个实数根;
(2)若方程的两根为x1,x2,且|x1|=|x2|,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB=12cm,点C在线段AB上,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB中点,求DE的长.
(2)若AC=4cm,求DE的长.
(3)若点C为线段AB上的一个动点(点C不与A,B重合),求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
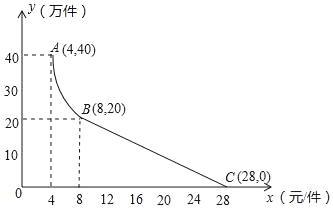
【题目】月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值.
(3)假设公司的这种电子产品第一年恰好按年利润s(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格x(元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润s(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )
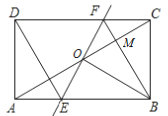
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为5,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.

(1)求证:PAPB=PDPC;
(2)若PA=![]() ,AB=
,AB=![]() ,PD=DC+2,求点O到PC的距离.
,PD=DC+2,求点O到PC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com