
【题目】如图,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为直角边且在
为直角边且在![]() 的右侧作等腰直角三角形
的右侧作等腰直角三角形![]() ,
,![]() ,
,![]() .
.

(1)如果![]() ,
,![]() .
.
①当点![]() 在线段
在线段![]() 上时,如图1,线段
上时,如图1,线段![]() 、
、![]() 的位置关系为___________,数量关系为_____________
的位置关系为___________,数量关系为_____________
②当点![]() 在线段
在线段![]() 的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动。探究:当
上运动。探究:当![]() 多少度时,
多少度时,![]() ?小明通过(1)的探究,猜想
?小明通过(1)的探究,猜想![]() 时,
时,![]() .他想过点
.他想过点![]() 做
做![]() 的垂线,与
的垂线,与![]() 的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
【答案】(1)①垂直,相等;②都成立;(2)当![]() 时,
时,![]()
【解析】
(1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;
②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立;
(2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图形判定△GAD≌△CAE,得出对应角相等,即可得出结论.
解:(1)①CE与BD位置关系是CE⊥BD,数量关系是CE=BD.
理由:如图1,∵∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,
∴∠BAD=∠CAE.
又 BA=CA,AD=AE,
∴△ABD≌△ACE (SAS)
∴∠ACE=∠B=45°且 CE=BD.
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,即 CE⊥BD.
故答案为:垂直,相等;
②都成立
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
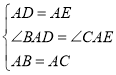
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ;
;
(2)当![]() 时,
时,![]() (如图).
(如图).

理由:过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
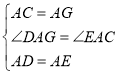
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程x2﹣6x﹣m=0有两个实数根.
(1)求m的取值范围;
(2)如果m取符合条件的最小整数,且一元二次方程x2﹣6x﹣m=0与x2+nx+1=0有一个相同的根,求常数n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列情境分别可以用图中哪幅图来近似地刻画?①一杯越晾越凉的水(水温与时间的关系);②一面冉冉上升的旗子(高度与时间的关系);③足球守门员大脚开出去的球(高度与时间的关系);④匀速行驶的汽车(速度与时间的关系),对应正确的是( )
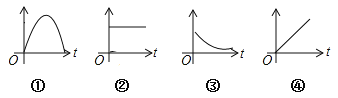
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.

(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为6cm,动点P从A点出发,在正方形的边上由A→B→C→D运动,设运动的时间为t(s),△APD的面积为S(cm2),S与t的函数图象如图所示
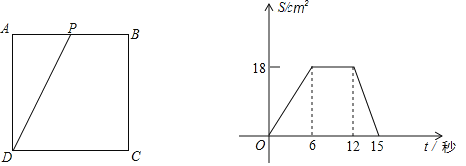
(1)求点P在BC上运动的时间范围;
(2)当t为何值时,△APD的面积为10cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x、y的二元一次方程组![]() 的解都为正数。
的解都为正数。
(1)求a的取值范围;
(2)化简|a+1||a1|;
(3)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求a的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com