
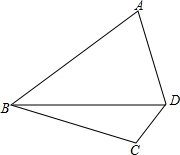
 如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.
如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.分析 (1)作∠DBM=∠BDA,∠BDN=∠DBA,射线BM,DN交于A′,△A′BD即为所求;
(2)由(1)中作图得知:∠A′BD=∠ADB,A′B=AD=15,A′D=AB=24,如图2,连接A′C,由∠ADB+∠CBD=90°,得到∠A′BD+∠CBD=90°,证得∠A′BC=90°,根据勾股定理得到A′C=25,根据勾股定理的逆定理得到△A′DC是直角三角形,于是得到结果.
解答 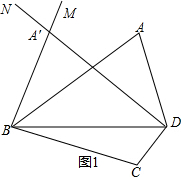 解:(1)如图1所示,△A′BD即为所求;
解:(1)如图1所示,△A′BD即为所求;
(2)由(1)中作图得知:∠A′BD=∠ADB,A′B=AD=15,A′D=AB=24,
如图1,连接A′C,
∵∠ADB+∠CBD=90°,
∴∠A′BD+∠CBD=90°,
即∠A′BC=90°,
∴A′B2+BC2=A′C2,
∵A′B=15,BC=20,
∴A′C=25,
在Rt△A′CD中,A′D=24,CD=7,
∴A′D2+CD2=576+49=625,
∵A′C2=625,
∴A′D2+CD2=A′C2.
∴△A′DC是直角三角形,且∠A′DC=90°,
∴${S_{四边形A'BCD}}={S_{△A'BC}}+{S_{△A'CD}}=\frac{1}{2}×20×15+\frac{1}{2}×24×7=234$,
∵S△A'BD=S△ABD,
∴S四边形ABCD=S四边形A'BCD=234.
点评 本题考查了全等三角形的判定和性质,勾股定理,三角形的面积,作图-复杂作图,正确的画出图形是解题的关键.


科目:初中数学 来源: 题型:解答题
| 月使用费/元 | 主叫限定时间/min | 主叫超时费/(元/min) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
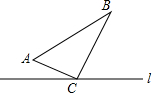 如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C路径向终点C运动;点Q从B点出发沿B-C-A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为1或$\frac{7}{2}$时,△PEC与△QFC全等.
如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A-C路径向终点C运动;点Q从B点出发沿B-C-A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为1或$\frac{7}{2}$时,△PEC与△QFC全等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a6•(-a)2=a | B. | 3a2•4ab=7a3b | C. | (-2x2)3=-6x6 | D. | (-a-b)2=(a+b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,若BC=10,CD=5$\sqrt{3}$-5.(结果保留根号)
一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,若BC=10,CD=5$\sqrt{3}$-5.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com