
 一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,若BC=10,CD=5$\sqrt{3}$-5.(结果保留根号)
一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,若BC=10,CD=5$\sqrt{3}$-5.(结果保留根号) 分析 过B作BG垂直于FC,由AB与CF平行,得到一对内错角相等,且得到三角形DEF与三角形BGD都为等腰直角三角形,利用30度所对的直角边等于斜边的一半求出BG的长,进而得出GD的长,利用勾股定理求出GC的长,由GC-GD求出CD的长即可.
解答 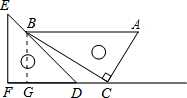 解:过B作BG⊥FC,交FC于点G,
解:过B作BG⊥FC,交FC于点G,
∵AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,
∴∠ABC=∠BCG=30°,△EDF和△BGD都为等腰直角三角形,即EF=DF,BG=DG,
∵BC=10,
∴BG=DG=$\frac{1}{2}$BC=5,
根据勾股定理得:CG=$\sqrt{B{C}^{2}-B{G}^{2}}$=5$\sqrt{3}$,
则CD=CG-GD=5$\sqrt{3}$-5.
故答案为:5$\sqrt{3}$-5.
点评 此题考查了勾股定理,含30度直角三角形的性质,以及等腰直角三角形,熟练掌握勾股定理是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
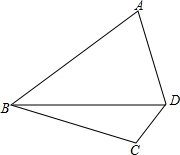 如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.
如图,已知四边形ABCD中,AB=24,AD=15,BC=20,CD=7,∠ADB+∠CBD=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
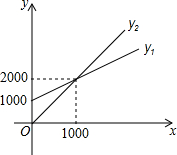 据报道,第九届中国-东盟博览会将于2012年9月21日至25日在南宁举行,为迎接东盟博览会,某企业计划要印刷该企业及其产品的宣传材料,甲印刷厂提出的收费方案是印刷费加制版费;乙厂提出的收费方案是只收印刷费,如图所示,y1为甲印刷厂的收费方案的图象,y2为乙印刷厂的收费方案的图象.
据报道,第九届中国-东盟博览会将于2012年9月21日至25日在南宁举行,为迎接东盟博览会,某企业计划要印刷该企业及其产品的宣传材料,甲印刷厂提出的收费方案是印刷费加制版费;乙厂提出的收费方案是只收印刷费,如图所示,y1为甲印刷厂的收费方案的图象,y2为乙印刷厂的收费方案的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
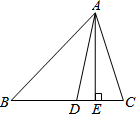 如图,在△ABC中,AE是BC边上的高,AD是角平分线.
如图,在△ABC中,AE是BC边上的高,AD是角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
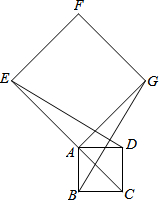 如图,在正方形ABCD中,延长对角线CA到点E,以AE为边作正方形AEFG,连接BG、DE.
如图,在正方形ABCD中,延长对角线CA到点E,以AE为边作正方形AEFG,连接BG、DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com