
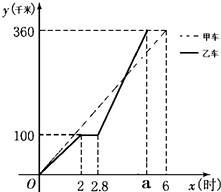
 甲、乙两车同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程y(千米)与行驶时间x(时)的函数图象如图所示.
甲、乙两车同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程y(千米)与行驶时间x(时)的函数图象如图所示.分析 (1)根据正比例函数解析式y=kx,代入(6,360)解答即可;
(2)将x=2.8代入正比例函数后,再减去100即可,根据题意得出乙的速度进行解答即可;
(3)得出解析式后,利用两直线相交进行解答即可.
解答 解:(1)设甲的解析式为:y=kx,把(6,360)代入解析式,
可得:k=60,
所以解析式为:y=60x;
(2)把x=2.8代入y=60x=168,
所以当x=2.8时,甲、乙两车之间的距离是168-100=68千米,
乙开始的速度为:100÷2=50千米/小时,
后来的速度为50×2=100千米/小时,
所以可设后来的解析式为:y=100x+b,
把(2.8,100)代入解析式y=100x+b,
可得:b=-180,
所以解析式为:y=100x-180,
把y=360代入y=100x-180,
解得:x=5.4,
故a=5.4,
故答案为:68;5.4;
(3)因为两直线y=60x和y=100x-180相交,联立方程可得:100x-180=60x,
解得:x=4.5,
答:行驶过程中,两车出发4.5小时首次后相遇.
点评 主要考查了函数图象的读图能力和函数与实际问题结合的应用.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
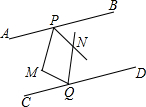 如图,M为两条平行线AB、CD之间的一点,P、Q分别在直线AB、CD上,∠BPM、∠DQM的平分线交于点N,若∠M=100°,则∠PNQ的度数为( )
如图,M为两条平行线AB、CD之间的一点,P、Q分别在直线AB、CD上,∠BPM、∠DQM的平分线交于点N,若∠M=100°,则∠PNQ的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com