
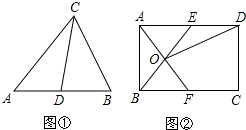
分析 (1)根据一组对边平行且相等的四边形是平行四边形,得到四边形ABFE是平行四边形,然后根据平行四边形的性质证得OE=OB,即可证得△AOE和△AOB是友好三角形;
(2)△AOE和△DOE是“友好三角形”,即可得到E是AD的中点,则可以求得△ABE、△ABF的面积,根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解.
探究:画出符合条件的两种情况:①求出四边形A′DCB是平行四边形,求出BC和A′D推出∠ACB=90°,根据三角形面积公式求出即可;
②求出高CQ,再求出△A′DC的面积,即可求出△ABC的面积.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∵AE=BF,
∴四边形ABFE是平行四边形,
∴OE=OB,
∴△AOE和△AOB是友好三角形.
(2)解:∵△AOE和△DOE是友好三角形,
∴S△AOE=S△DOE,AE=ED=$\frac{1}{2}$AD=6,
∵△AOB与△AOE是友好三角形,
∴S△AOB=S△AOE,OB=OE,
在△AOE与△FOB中,
$\left\{\begin{array}{l}{AE=BF}\\{∠AEO=∠OBF}\\{OB=OE}\end{array}\right.$,
∴△AOE≌△FOB(SAS),
∴S△AOE=S△FOB,
∴S△AOD=S△ABF,
∴S四边形CDOF=S矩形ABCD-2S△ABF=8×12-2×$\frac{1}{2}$×8×6=48;
探究:
解:分为两种情况:①如图1所示,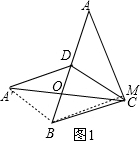 ∵S△ACD=S△BCD.
∵S△ACD=S△BCD.
∴AD=BD=$\frac{1}{2}$AB,
∵沿CD折叠A和A′重合,
∴AD=A′D=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2,
∵△A′CD与△ABC重合部分的面积等于△ABC面积的$\frac{1}{4}$,
∴S△DOC=$\frac{1}{4}$S△ABC=$\frac{1}{2}$S△BDC=$\frac{1}{2}$S△ADC=$\frac{1}{2}$S△A′DC,
∴DO=OB,A′O=CO,
∴四边形A′DCB是平行四边形,
∴BC=A′D=2,
过B作BM⊥AC于M,
∵AB=4,∠BAC=30°,
∴BM=$\frac{1}{2}$AB=2=BC,
即C和M重合,
∴∠ACB=90°,
由勾股定理得:AC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴△ABC的面积是$\frac{1}{2}$×BC×AC=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$;
②如图2所示,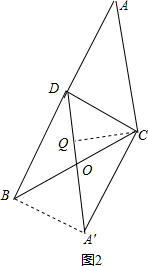 ∵S△ACD=S△BCD.
∵S△ACD=S△BCD.
∴AD=BD=$\frac{1}{2}$AB,
∵沿CD折叠A和A′重合,
∴AD=A′D=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2,
∵△A′CD与△ABC重合部分的面积等于△ABC面积的$\frac{1}{4}$,
∴S△DOC=$\frac{1}{4}$S△ABC=$\frac{1}{2}$S△BDC=$\frac{1}{2}$S△ADC=$\frac{1}{2}$S△A′DC,
∴DO=OA′,BO=CO,
∴四边形A′BDC是平行四边形,
∴A′C=BD=2,
过C作CQ⊥A′D于Q,
∵A′C=2,∠DA′C=∠BAC=30°,
∴CQ=$\frac{1}{2}$A′C=1,
∴S△ABC=2S△ADC=2S△A′DC=2×$\frac{1}{2}$×A′D×CQ=2×$\frac{1}{2}$×2×1=2;
即△ABC的面积是2或2$\sqrt{3}$.
点评 本题是四边形综合题目,考查了平行四边形性质和判定、全等三角形的判定与性质、三角形的面积的计算、勾股定理、含30°角的直角三角形的性质;本题难度较大,综合性强,需要进行分类讨论才能得出结果.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
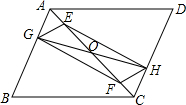 如图所示,已知,在?ABCD中,点E,F在AC上,且AF=CE,点G,H分别在AB,CD上,且AG=CH,AC与GH相交于点O,求证:四边形EGFH是平行四边形.
如图所示,已知,在?ABCD中,点E,F在AC上,且AF=CE,点G,H分别在AB,CD上,且AG=CH,AC与GH相交于点O,求证:四边形EGFH是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com