
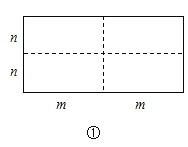
【题目】如图①是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)图②中的阴影部分的面积为
(2)观察图②,请你写出代数式![]() 与
与![]() 之间的等量关系式
之间的等量关系式

(3)若![]() 则
则![]()
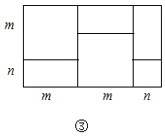
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示
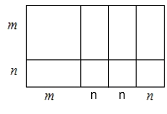
(5)试画出一个几何图形,使它的面积能表示![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() ;(5)见解析
;(5)见解析
【解析】
(1)②中的阴影部分为边长为(m-n)的正方形,然后根据正方形面积公式求解即可;
(2)由于图②中阴影部分的面积可以表示为![]() 或
或![]() ,整理即可;
,整理即可;
(3)利用(2)的结论得到![]() ,再把
,再把![]() ,
,![]() 代入计算,然后根据平方根的定义求解;
代入计算,然后根据平方根的定义求解;
(4)利用图形的面积不变得到列等式即可得到结果;
(5)先拼接![]() 的长方形,然后利用面积之间的关系得到.
的长方形,然后利用面积之间的关系得到.
解: (1)观察发现②中的阴影部分为边长为(m-n)的正方形,
∴阴影部分的面积为![]() ;
;
(2)观察图②,发现图②中阴影部分的面积可以表示为![]() 或
或![]() ,
,
∴![]() ;
;
(3)![]() ;
;
把![]() ,
,![]() 代入
代入
![]()
![]() ,
,
∵m>n,
∴![]()
故:答案为![]() ;
;
(4)观察图③,可以根据面积不变可以得到,
![]() ,
,
(5)先拼接![]() 的长方形,发现面积正好为1个边长为m的正方形,4个长宽分别为m、n的矩形以及3个边长为n的正方形的面积和,
的长方形,发现面积正好为1个边长为m的正方形,4个长宽分别为m、n的矩形以及3个边长为n的正方形的面积和,
即![]() ,
,
如下图所示:


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
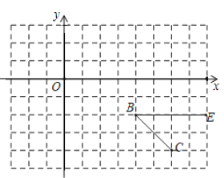
【题目】如图,平面直角坐标系中,![]()
![]() 轴,点
轴,点![]() 从原点
从原点![]() 出发在
出发在![]() 轴上以
轴上以![]() 单位/秒的速度向
单位/秒的速度向![]() 轴的正方向运动,运动的时间为
轴的正方向运动,运动的时间为![]() 秒.
秒.![]() 平分
平分![]() . (提示:
. (提示:![]() 中,
中,![]() ,若
,若![]() 则
则![]() ,反之亦然)
,反之亦然)
(1)当![]() 时,
时,![]() ;
;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 点运动的时间
点运动的时间![]() ;
;
(3)当![]() 时,求
时,求![]() 的度数(用含
的度数(用含![]() 的式子表示,且不含绝对值).
的式子表示,且不含绝对值).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(—3,—3),B(—2,—1),C(—1,—2)是直角坐标平面上三点。

(1)请画出ΔABC关于原点O对称的ΔA1B1C1,
(2)请写出点B关天y轴对称的点B2的坐标,若将点B2向上平移h个单位,使其落在ΔA1B1C1内部,指出h的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,双曲线
中,双曲线 ![]() 与直线
与直线 ![]() 交于点A(3,1).
交于点A(3,1).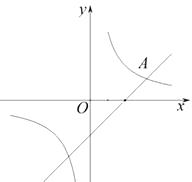
(1)求直线和双曲线的解析式;
(2)直线 ![]() 与x轴交于点B,点P是双曲线
与x轴交于点B,点P是双曲线 ![]() 上一点,过点P作直线PC∥x轴,交y轴于点C,交直线
上一点,过点P作直线PC∥x轴,交y轴于点C,交直线 ![]() 于点D.若DC=2OB,直接写出点
于点D.若DC=2OB,直接写出点 ![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
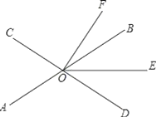
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.3m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过计算说明.(参考数据:![]() ≈1.7)
≈1.7)
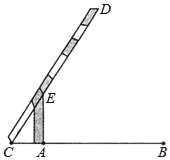
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com