
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF为( ) 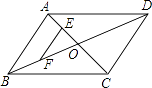
A.3厘米
B.4厘米
C.5厘米
D.6厘米
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
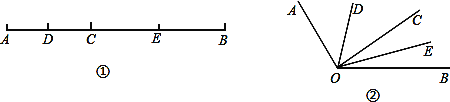
【题目】如图①,已知线段AB=12cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若AC=4cm,求DE的长;
(2)试利用“字母代替数”的方法,说明不论AC取何值(不超过12cm),DE的长不变;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF。设CE=a,CF=b。
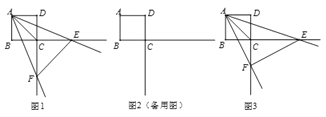
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一幅三角板按照如图所示的位置放置在直线![]() 上,
上, ![]() =
=![]() =45°,
=45°,![]() =
=![]() =90°,
=90°,![]() =30°,
=30°,![]() =60°.将含45°锐角的三角板
=60°.将含45°锐角的三角板![]() 固定不动,含30°锐角的三角板
固定不动,含30°锐角的三角板![]() 绕点
绕点![]() 顺时针旋转1周,在此过程中:
顺时针旋转1周,在此过程中:
(1)如图,当点![]() 在
在![]() 内部时,连接
内部时,连接![]() .
.
①若![]() 平分
平分![]() ,试问
,试问![]() 是否也平分
是否也平分![]() ?请说明理由.
?请说明理由.
②若![]() ,
, ![]() ,
, ![]() ,试探究
,试探究![]() 、
、![]() 、
、![]() 这三者之间有什么数量关系?请用一个含
这三者之间有什么数量关系?请用一个含![]() 、
、![]() 、
、![]() 的等式来表达,并说明理由.
的等式来表达,并说明理由.
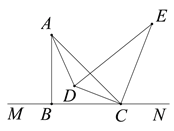
(2)如图, ![]() 是
是![]() 的角平分线,当
的角平分线,当![]() 所在直线与
所在直线与![]() 所在直线互相垂直时,请直接写出
所在直线互相垂直时,请直接写出![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年消费者的旅游消费不断升级。根据国家旅游局数据中心综合测算,2017年春节期间,全国共接待游客3.44亿人次,实现旅游总收入4233亿元。将4233亿用科学记数法表( )
A.4.233×109
B.4.233×1010
C.4.233×1011
D.4.233×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
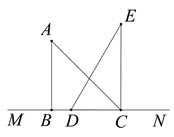
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
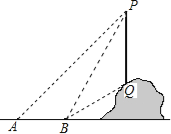
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多项式﹣x+x3+1﹣x2按x的升幂排列正确的是( )
A.x2﹣x+x3+1
B.1﹣x2+x+x3
C.1﹣x﹣x2+x3
D.x3﹣x2+1﹣x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同,甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)求甲、乙每天各加工零件多少个?
(2)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com